
통계는 현명한 의사결정을 하는데 도움을 줍니다. 불확실한 현실 세계에서 보이지 않던 것들을 보게 해주고, 과학적 근거의 틀을 마련해 미래에는 과거보다 더 나은 선택을 할 수 있도록 도와줍니다. 빠르게 변화하는 현대 사회에서 통계를 이해하고 활용하는 일은 중요합니다.
이처럼 통계를 이용해 현실을 깊이 이해하는 통찰력을 데이터 문해력(data literacy)이라고 합니다. 영국의 통계학자 데이비드 스피겔할터(David Spiegelhalter)는 데이터 문해력에 대해 다음과 같이 정의합니다.
불확실한 현실 세계에서 현실 세계 문제에 관한 통계를 해석하는 능력, 다른 사람이 도출한 통계적 결론을 이해하고 비판적으로 분석하려는 능력
데이터 문해력의 기초는 정확한 용어를 사용하는데서 시작합니다. 우리가 의사결정모델이라는 집을 짓는다면, 정확한 용어는 집을 이루는 기초 철근 구조물과도 같습니다. 용어를 정확하게 이해하고 사용할수록 기반이 단단한 집을 지을 수 있습니다.
이번 시간에는 확률과 통계에서 사용하는 주요 용어를 살펴보겠습니다. 글에서 다룬 용어는 머신러닝과 딥러닝에서도 자주 사용됩니다. 각 용어 카드에는 용어의 국문명, 영문명, 기호, 정의, 공식, 특징, 예제가 함께 제시되어 있습니다. 글에서 다룬 주요 정의는 참고 문헌에 있는 전문 통계학 도서와 온라인 강의 자료 및 교양 통계 도서에서 차용하였습니다. 내용은 지속적으로 업데이트될 예정입니다.
집합
정의
원소(elements) 또는 구성원(members)의 모임
- 원소의 순서는 의미가 없음 {1, 3, 5} = {3, 5, 1}
- 알파벳 대문자로 표기
집합을 이루는 개별 사물, (수학적) 개체
- 알파벳 소문자로 표기
표기법
기본
원소를 나열하여 집합을 나타내는 표기법
- {a, e, i, o, u}
- {흰색, 검은색}
- {1, 4, 9, 16, …}
어떤 집합을 그 집합의 원소들이 만족하는 성질(조건)을 서술(제시)함으로써 나타내는 표기법
- {x|x는 홀수, x < 5}
- {x|x = k^2, k는 자연수}
- {x^2|x는 자연수}
- 순서 중요
수체계
두 정수의 비율 또는 분수의 형식으로 나타낼 수 있는 수
두 정수의 비의 형태로 나타낼 수 없는 실수, 분수로 나타낼 수 없는 소수
실수와 허수의 합의 꼴로써 나타내는 수
구간
그림
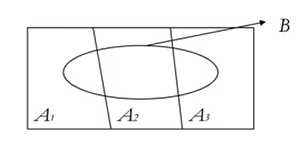
겹치는 원 또는 기타 모양을 사용하여 두 개 이상의 항목 집합 간의 논리적 관계를 설명하는 그림
크기
집합의 크기(cardinality)는 집합을 이루는 구성 원소의 수입니다. 집합의 크기는 '||'로 나타냅니다.
유한개의 원소로 이루어진 집합, 집합의 원소를 셀 수 있는 집합
무한개의 원소로 이루어진 집합, 집합의 원소를 셀 수 없는 집합
종류
특정한 문제에서 가능한 모든 원소의 집합
모든 원소 중 일부를 나타내는 집합
- 집합 E의 모든 원소가 집합 S의 원소이면 E는 S의 부분집합
부분 집합 중 자기 자신은 원소로 갖지 않는 집합
위의 집합 A 중 그 자신인 A집합
위의 집합 중 W는 A의 초 집합
어떠한 원소도 갖지 않는 집합
- |Ø| = 0
- |{Ø}| = 1
전체 집합 U에 속하나 A에는 속하지 않는 집합
집합 A에 대해 모든 가능한 부분 집합들의 집합
- S = {1, 2}, P(S) = {Ø, {1}, {2}, {1,2}}
어떤 집합을 서로소(disjoint)가 되도록 조각/분리/나누는 것, 멱집합 중의 특정한 부분 집합
- {1, 3, 5}와 {2, 4, 6}은 서로소
연산
정의
덧셈, 뺄셈, 곱셈과 같은 수의 연산처럼 집합 간에 취해지는 연산
- 여러 집합 간의 연산으로 새로운 집합을 만드는 것
종류
집합 A 또는 집합 B에 속하는 원소들로 구성된 집합
- 논리연산 OR에 해당
집합 A와 집합 B에 공통적으로 속해 있는 원소만을 포함하는 집합
- 논리연산 AND에 해당
- {1,2} ∩ {1,3,4} = {1,3}
집합 A에는 속하나 집합 B에는 속하지 않는 원소들의 집합
- {1,2} - {1,3,4} = {2}
두 집합 A,B의 원소들로 만들어지는 모든 (a,b)들의 집합, a∈A 이고 b∈B에 대해 모든 순서쌍 (a,b)들의 집합
- 카테시안 곱의 크기, 즉 가능한 모든 순서쌍의 개수는 두 집합 A,B 곱의 크기는 각각의 크기를 곱한 것과 같음
- A = {1,2}, B = {a,b} 이면, A x B = {(1,a),(1,b),(2,a),(2,b)}
- 2차원 실수 공간: 2차원 실수 순서쌍 전체의 집합 = 평면상의 모든 점들의 집합 = 모든 실수 순서쌍들의 집합 R^2 = R × R = {(x,y)|x,y : 실수 }
법칙
두 집합의 합집합의 보집합은 각각의 집합의 보집합의 교집합과 같음
두 집합의 교집합의 보집합은 각각의 집합의 보집합의 합집합과 같음
순열과 조합
대상이 되는 요소들의 배치(배열)에 대해 연구하는 수학의 한 분야, 다양한 패턴으로 나열하는(조합시키는) 방법을 연구하는 학문
기초
시행(trial)을 통해 일어날 수 있는 사건(event)의 가짓수
수(경우의 수)를 세는 방법, 어떤 사건(event)이 발생할 수 있는 경우의 수를 계산하는 것
- 덧셈: 하나씩 세는 것
- 곱셈: 똑같은 덧셈이 몇 번인가를 세는 것
규칙
원소들이 서로소(Disjoint, X ∩ Y=0) 또는 상호배타적인 부분집합으로 나누어질 때 각 부분집합의 원소의 개수를 합하면 전체가 됨
각 사건에서의 발생 가능한 경우의 수 n을 모두 곱하면 전체 경우의 수와 같아짐
- n개의 비트로 표현 가능한 총 경우의 수 = 2^n
개념
순열
서로 다른 n개의 객체를 나열하는 경우의 수
서로 다른 n개의 객체 중에서 r개의 객체를 중복을 허락하지 않고 순서를 고려하면서 선택하는 경우의 수
n개의 서로 다른 객체 중에서 r개를 중복을 허용하여 뽑아서 한 줄로 나열하는 경우의 수
조합
서로 다른 n개의 객체 중에서 r개의 객체를 순서를 고려하지 않고 선택하는 경우의 수
- n choose r 이라고 함
정리
이항의 거듭제곱을 전개하여 다항식을 구하는 정리
- 파스칼의 삼각형(Pascal's triangle)
다항의 거듭제곱을 전개하여 다항식을 구하는 정리
서로 다른 n개의 객체 중에서 r개를 뽑는 경우의 수
n개의 객체 중에서 r개로 그룹 지어 구분하는 경우의 수
확률
용어
실험
데이터를 생성해내는 모든 과정
- 데이터 수집 방법의 하나인 실험과 동일한 의미
- 동전 던지기
- 주사위 던지기
- 마트의 방문 고객 수 세기
표본공간
실험으로부터 나온 모든 결과를 담고 있는 집합, 실험이나 관찰에서 생길 수 있는 모든 사건의 모임, 측정 가능한 모든 결과의 집합
- 표본점(sample): 표본 공간을 이루는 개개의 관찰 결과
- 우리가 수집한 표본은 표본 공간의 부분집합
표본공간 안에 담겨 있는 집합의 원소가 이산형인 표본공간
- 1개의 동전 던지기: S = {H, T}
- 주사위 던지기: S = {1, 2, 3, 4, 5, 6}
표본공간 안에 담겨 있는 집합의 원소가 연속형인 표본공간
- 0에서 100 사이의 모든 숫자: S = {x|0 < x < 100}
- 반지름이 2인 모든 원 위의 점: S = {(x, y)|x^2 + y^2 = 4}
사건
표본공간의 부분집합으로 어떤 조건을 만족하는 특정한 표본점들의 집합, 실험이나 관찰에서 얻은 결과
- 주사위를 던졌을 때 홀수가 나오는 경우의 수: E = {odd number} = {1, 3, 5}
여러 개의 사건 가운데 한 개의 사건
교집합이 없는 사건
정의
어떤 사건이 일어날 가능성
- 상대적 비율 또는 상대적 빈도로 표현할 수 있음
어떤 사건이 나타날 확률은 실험을 무한에 가깝게 계속적으로 시행했을 때 전체 시행횟수에서 그 사건이 나타나는 빈도수, 동일한 조건 하에서 동일한 실험을 무수히 반복해서 시행할 때 나올 수 있는 모든 경우의 수(표본공간) 중 어떤 특정 사건이 발생하는 비율
- : A사건이 발생할 확률
- : 총 시행횟수
- : A사건이 발행한 횟수
어떤 실험이나 관찰의 결과로 나타날 수 있는 모든 경우들이 각각 동일한 가능성을 가지고 발생할 것이라는 가정하에서 특정 사건 A가 일어날 확률을 정의한 것, 전체의 경우 중에서 어떤 특정사건이 차지하는 경우의 구성 비율(proportion)과 같은 의미를 지님
- 확률 = 구성 비율
종류
누가 계산해도 동일한 값이 나오는 엄밀한 확률
= 선험적 확률, 이론적 확률동일 조건/독립적으로 몇 번 반복하였을 때의 발생 확률(도수 이론:frequency theory)
= 통계적 확률, 상대빈도확률, 객관적 확률관찰자의 주관적 믿음/확신으로써 표현되는 확률
- 베이즈확률: 모집단을 미리 확정짓지 않고, 모수를 마치 확률변수처럼 취급
표본공간에서 각 사건에 대한 확률이 동일한 것
- : 표본공간의 원소수
바로 전의 실험결과에 의해 변화된 표본 공간에서 어떤 사건이 일어날 확률, 사건 B가 발생했다는 조건하에서 사건 A가 발생할 확률
확률측도
전체 중의 부분집합(사건)에 숫자를 대응시킨 함수
공리와 법칙
공리
- : 표본공간
- 공리1: 실험으로부터 나온 모든 결과에 대한 확률은 0과 1사이에 있다
- 공리2: 표본공간 S 안에 있는 점(point), 즉 사건이 나올 확률의 합은 1이다
- 공리3: 상호배타적인 사건들의 합집합에 대한 확률은 각 사건에 대한 확률을 더한 것과 같다, 상호배타적인 사건들에 대하여 적어도 하나의 사건이 발생할 확률은 각각의 확률의 합이다
법칙
집합이론의 합집합 개념에 대응되는 확률
집합이론의 교집합 개념에 대응되는 확률
- 사건 A와 B가 동시에 일어날 확률은 사건 A가 일어날 확률과 사건 A가 일어난 다음 사건 B가 일어날 확률을 곱한 것과 같음
사전확률과 사전정보 조건부확률을 바탕으로 사후확률을 계산하는 법칙
- : 정보
- : 사전확률(prior probability)
- : 사전정보 조건부확률(data probability)
- : 사후확률(posterior probability)
- 사후확률은 사전확률의 업데이트 버전과 같음
- 실험의 결과로써 얻은 정보를 토대로 하여 어떤 사건의 알려져 있지 않은 확률을 구하려고 하는 가장 간단한 방법
사건 A가 발생하지 않을 경우 대비 발생할 확률
- 성공 확률이 1일 경우: 오즈는 무한대의 값
- 성공 확률이 0일 경우: 오즈는 0의 값
- 피파의 대한민국 오즈 500:1, 1/500: 1달러를 걸었을 때 배당금 500달러를 받음 = 우승확률이 1/501로 약 0.001996(0.1996%)
종속과 독립
처음에 어떤 결과가 나왔느냐 하는 것이 다음에 어떤 사건이 발생할 확률에 아무 영향을 주지 않는 경우, 사건 A가 나올 확률은 사건 B의 결과에 관계없이 언제나 같음
- 복원추출
조건부 확률처럼 한 사건의 발생이 다음에 발생할 사건에 영향을 주는 경우
- 비복원추출
추첨 후 다음번에도 중복 추출이 가능하도록 해당 샘플을 다시 모집단에 포함시키는 추출
한번 뽑힌 원소는 추후 추첨에 사용하지 않는 추출
- 흰공과 검은공이 있을 때 비복원 추출로 두 번 모두 흰공이 나올 확률
- 사건 A와 사건B가 독립이면, 사건 A와 사건 B의 여집합도 독립
- 흰공과 검은공이 있을 때 복원 추출로 두 번 모두 흰공이 나올 확률
확률변수
정의
표본 공간의 모든 원소(X)를 실수(Y)로 대응시키는 함수, 실험으로부터 나온 표본(실험 결과)들을 실수로 변환하는 함수, 일정한 확률을 가지고 발생하는 사건(확률시행으로 인해 나타날 수 있는 여러 사건)을 수치로 변환하는 함수, 무작위 실험을 했을 때 특정 확률로 발생하는 각각의 결과에 그에 상응하는 실숫값을 부여하는 변수, 확률 실험에서 나올 수 있는 모든 결과를 대변하는 변수
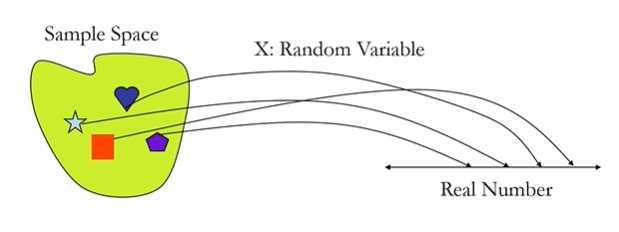
- 입력(input): 표본 공간의 모든 원소들(실험으로 부터 나온 각각의 결과들), 출력(output): 실수
- 상태공간(state space): 확률변수 X가 취하는 모든 실수들의 집합
- 표본공간 -> 실수공간
- X: 동전을 두 번 반복해서 던지는 게임에서 앞면이 나온 횟수
종류
확률변수는 실험으로부터 나온 개별 결과들을 실수로 변환할 때 필요한 함수가 확률변수입니다. 이때 실수가 이산적 값이면 이산확률변수(discrete random variable), 셀 수 없는 연속적 값이면 연속확률변수(continuous variable)입니다.
확률변수가 취할 수 있는 값의 수가 유한하거나 무한하더라도 셀 수 있는 확률변수, 상태공간이 유한 집합 또는 셀 수 있는 무한집합인 확률변수
- 확률의 총합은 더하기(Σ), 확률변수가 가질 수 있는 값이 유한함(이산형)
- 동전 던지기에서 동전 앞면이 나온 횟수
확률변수가 취할 수 있는 값이 일정한 구간 내의 실수로서 그 수가 무한한 확률변수
- 확률의 총합은 적분(∫), 확률변수가 가질 수 있는 값이 무한함(연속형)
- 제품의 중량
- 대한민국 국민의 평균 소득
- 학생들의 키
- 미국 주식 시장의 다우존스 지수
이때 확률변수의 출력값인 각각의 실수가 실제로 나올 가능성을 표현해주는 수학적 방법이 바로 확률함수(probability function)입니다.
확률함수
정의
확률변수로부터 나온 실수를 0~1사이의 확률값으로 바꿔주는(대응시키는) 함수, 확률의 흩어짐을 표현하는 함수, 확률변수가 어떤 특정 실수를 취할 것인지에 대한 확률을 나타내는 함수, 확률변수가 일어날 확률을 나타내는 함수
- 확률변수가 분포하는 형태를 함수적으로 보여줌
- 입력(input): 확률변수가 취하는 실수
- 출력(output): 확률
- 0과 1 사이의 값
- 실수공간 -> 확률
통계학에서는 이 확률함수를 확률변수의 출력값의 유형, 즉 확률함수의 입력값이 이산형인지 연속형인지에 따라 다른 이름을 사용합니다. 이산확률변수가 취하는 확률함수를 확률질량함수(probability mass function, PMF)라 하고, 연속확률변수가 취하는 확률함수를 확률밀도함수(probability density function, PDF)라고 합니다.
종류
이산확률변수의 확률분포를 표현하는 함수, 이산확률변수에서 특정 값에 대한 확률을 나타내는 함수, 이산확률변수 X의 분포를 나타내는 함수
- : 확률변수
- : 확률변수가 취할 수 있는 이산형 값
- : 확률변수 X가 특정한 값을 가질 확률
- p.m.f 값 = 함수값 = 확률
연속확률변수의 확률분포를 표현하는 함수, 연속확률변수에서 확률변수가 취할 수 있는 모든 값에 대해 그 값을 가질 확률이 얼마인지를 알려주는 함수, 확률변수의 분포를 나타내는 함수, 연속확률분포의 양상을 나타내는 곡선을 식으로 표현한 것, 연속확률변수 X의 분포를 나타내는 함수
- 확률밀도함수 f(x)는 특정한 한 순간에서의 확률은 0
- 하지만 특정 구간에서는 확률의 의미를 갖음
- 함수 아래의 면적 = 확률
확률질량함수와 확률밀도함수는 누적분포함수를 통해 쉽게 유도할 수 있습니다. 누적분포함수가 불연속함수일 때는 누적분포함수의 특정 값끼리 뺄셈을 하면 확률질량함수를 구할 수 있습니다. 만일 누적분포함수가 연속함수일 때는 누적분포함수를 미분해서 확률밀도함수를 구할 수 있습니다. 다시 말해 이산확률분포의 확률질량함수에서 부터 특정 값 사이에 있는 모든 확률변수에 대한 확률을 더하거나 연속확률분포의 확률밀도함수를 적분하면 누적분포함수가 됩니다.
확률변수와 그 확률변수가 있는 값 이하의 값을 취하는 확률과의 관계를 나타낸 함수, 주어진 확률 변수가 특정 값보다 작거나 같은 확률을 나타내는 함수, 주어진 확률변수에서의 누적 확률을 나타내는 함수, 특정값 x에 대해 확률변수 X가 x보다 같거나 작은 모든 경우의 확률의 합
- pdf는 cdf의 미분값
- cdf는 단조증가함수
ECDF는 n개의 데이터 포인트 각각에서 1/n 씩 점프하는 계단 함수
= 누적분포함수(cumulative density function, CDF)어떤 한 점의 x값 이상의 모든 x값들이 갖는 비율을 누적한 값
지금까지 확률변수와 확률함수의 개념을 살펴보았습니다. 확률변수와 확률함수를 이용하면 특정 사건이 일어날 확률을 계산할 수 있습니다. 그리고 확률변수의 모든 값과 각 확률변수의 값에 대응하는 모든 확률들의 분포를 그림으로 나타낸 것이 확률분포(probability distribution)입니다.
확률분포의 개념을 알아보기 전에 먼저 확률변수로부터 실수가 얻어졌을 때 이 실수들을 요약하는 방법이 있습니다. 이 방법이 기댓값(expected value)과 분산(variance)입니다. 기댓값은 실수들의 중심 경향성을 파악할 수 있도록 돕고 분산은 실수들이 흩어진 정도를 알 수 있도록 도와줍니다.
요약값
기댓값
확률변수가 취할 수 있는 모든 값들의 평균, 확률분포의 성격을 결정짓는 확률적 평균치, 확률변수가 나타내는 확률분포에서 중심 위치에 있는 대표적인 값, 모든 값이 동일하게 나온다는 가정을 가진 특별한 기댓값인 산술평균(average) 또는 확률변수에 취해지는 확률적 가중평균(weighted average)과 같은 개념, 범주에 해당하는 어떤 수치가 있을 때 범주의 출현 확률(probability)에 따른 평균, 모집단에 대한 통계적 파라미터 중 하나로써 기대되는 예측치들의 평균값으로 모집단 확률분포의 모수에 대한 무게중심으로 기대되는 값, 기대값은 매 표본 집단마다 얻어지는 표본 평균들에 대한 일반화, 시행횟수가 무한해지면 대수의 법칙에 따라 표본평균은 모집단(확률변수)의 기댓값에 수렴
- 확률분포의 집중화경향을 알고 싶을 때
- : 확률변수로부터 나온 실숫값
- : 각 실숫값에 해당하는 확률
기댓값은 통계량(statistic)에서 다룰 평균(means)과 다른 개념입니다. 기댓값에서는 각 사건들이 일어날 확률이 모두 다릅니다. 그래서 확률변수가 취할 수 있는 모든 값, 기대되는 예측치들의 평균값을 내는 것입니다. 반면 평균에서는 각 사건들이 일어날 확률이 모두 동일하게 나온다고 가정합니다. 평균에 대한 개념은 통계적 기술의 위치통계를 참조하시면 됩니다.
분산
확률변수들이 기댓값 E(X)로부터 얼마나 떨어져 있는가를 나타내는 것
- 확률분포의 분산도를 알고 싶을 때
특정 집단 내 데이터들의 표준편차
- 개별 데이터 포인트의 변동성을 측정하는 지표
- 확률분포의 표준편차를 알고 싶을 때
확률변수는 표본 공간의 모든 원소를 실수로 대응시키고, 확률함수는 이 실수들이 나오는 확률을 나타냅니다. 이 실수들이 나오데는 어떤 패턴이 있습니다. 확률분포(probability distribution)는 확률함수로부터 확률변수가 된 각 실숫값이 나올 확률들의 패턴입니다.
확률분포
정의
확률함수의 각 실수값이 취하는 확률값들이 이루는 패턴, 확률함수로부터 생성된 확률값들의 패턴, 확률변수의 모든 값과 그에 대응하는 확률들이 나타내는 분포, 어떤 확률변수가 취할 수 있는 모든 값들과 이 값들이 나타날 확률을 나타내는 것, 한 변수에 대해 어떤 실험이나 관찰의 결과로 나타날 수 있는 모든 상황과 각 상황이 나타날 확률을 나타내는 것, 확률변수가 취하는 값에 대해 합이 1인 확률이 어떻게 분포되어 있는지를 나타내는 것, 한 변수가 어떤 실험이나 관찰의 결과로 나타날 수 있는 모든 상황과 각 상황이 나타날 확률을 나타내는 것
- 확률함수가 확률분포를 정함
종류
이산확률변수의 확률분포, 이산형 확률함수로부터 나온 확률들의 패턴
= 이산형 확률분포연속확률변수의 확률분포, 연속형 확률함수로부터 나온 확률들의 패턴
= 연속형 확률분포이산확률분포와 연속확률분포의 가장 큰 차이점은 확률을 로 표현할 수 있는지의 여부입니다. 이산확률변수는 로 가능합니다. 하지만 연속확률변수는 불가능합니다. 연속확률변수에서는 처럼 범위로 표현해야 합니다.
또한, 각 확률분포의 세부적인 모양은 모수(parameters)에 의해 결정됩니다. 모든 확률함수에는 하나 이상의 파라미터가 존재합니다.
지금까지는 하나의 확률변수에 대한 확률분포를 알아보았습니다. 이와 다르게 한 실험에서 두 개 이상의 확률변수가 상호작용면서 만들어지는 확률분포가 있습니다. 바로 결합확률분포(joint probability distribution)와 주변확률분포(marginal probability distribution)입니다.
결합확률분포와 주변확률분포
결합확률함수로부터 나오는 확률 패턴
- 두개의 확률변수가 각 실수로 대응되는 확률을 구하고 싶을 때 사용
- : 결합확률함수
- : 확률변수 X가 x를 갖고 확률변수 Y가 y를 동시에 갖을 확률
- 결합확률함수(joint probability function): 두 개의 확률변수가 어떤 특정 실수값을 동시에 가질 때의 확률을 나타내는 함수
확률변수 X와 확률변수 Y의 결합분포에서 X 또는 Y의 어느 하나만의 확률분포, 결합확률분포의 주변(margin)에 표시되는 확률분포
- : 주변확률함수(marginal probability function)
두 개의 실수 집합 A, B가 다음 전제를 만족시킬 때 독립인 확률변수 X, Y
- 확률변수 X와 Y가 독립이면, 두 확률변수는 서로 영향을 주지 않음
확률변수 X+Y의 누적확률함수
- 컨볼루션(cdf)을 미분해서 pdf를 구함
- 컨볼루션을 미분한 pdf를 통해 두 확률변수의 합의 확률분포를 알 수 있음
이산확률분포와 연속확률분포의 종류는 다음과 같습니다.
이산확률분포
확률변수 X가 두 개의 값(성공과 실패)만을 갖을 때 확률분포, 베르누이 확률변수의 확률분포, 베르누이 확률함수로부터 생성되는 확률들의 패턴
- : 성공 확률
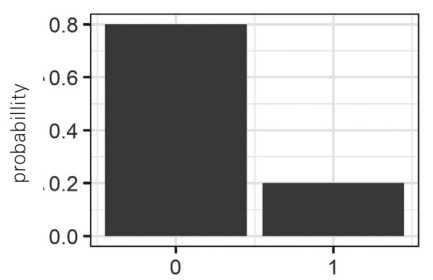
- 베르누이 시행을 n번 해서 나타나는 확률분포가 이항분포
- 동전을 던져서 앞이 나올지 뒤가 나올지
- 상품의 구매 여부
- 약의 효과 유무
- 시행(trial)
- 독립된 결과를 가져오는 하나의 사건
- 성공(success)
- 시행에 대한 관심의 결과
- 베르누이 시행(bernoulli trials)
- 어떤 실험의 결과가 2가지인 시행(성공/실패, 예/아니오, 0/1, 이진)
- 베르누이 확률변수(bernoulli random variable)
- 매 시행마다 오직 두 가지의 가능한 결과만 일어난다고 할 때 실험을 1회 시행하여 일어난 두 가지 결과(성공 또는 실패)에 의해 그 값이 각각 0과 1로 결정되는 확률변수
성공 확률이 p로 일정한 베르누이 시행을 독립적으로 n번 반복했을 때 주어진 시행 횟수(n) 중에서 성공한 횟수(x)의 도수분포, 이항확률변수의 확률분포
- : 성공 확률
- : 시행 횟수
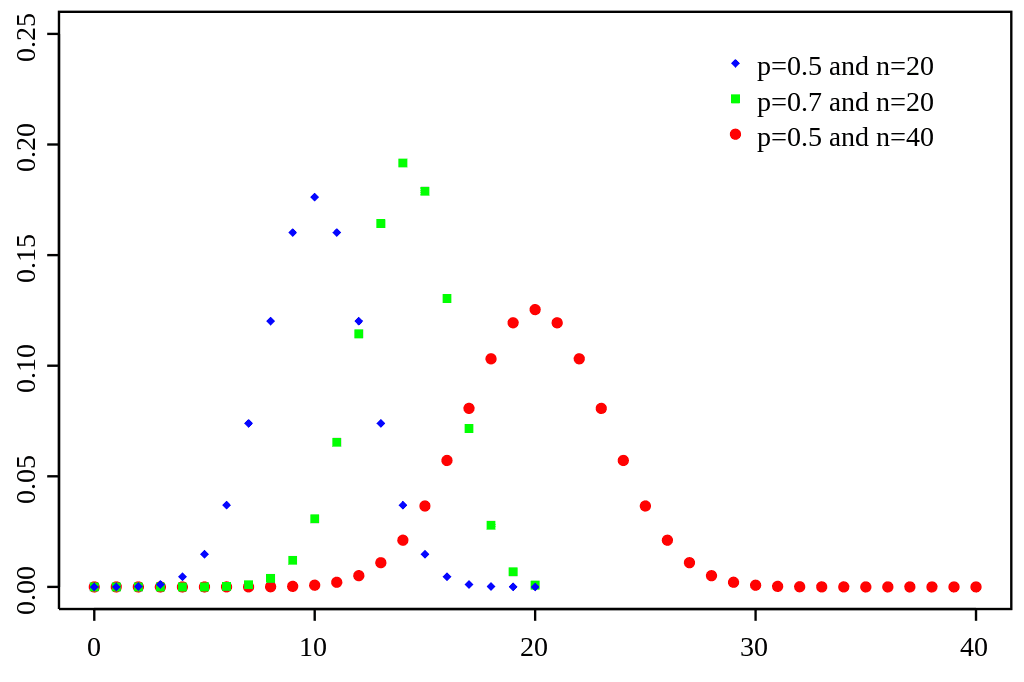
- p(x)는 0과 1 사이의 확률
- 이항확률변수(binominal random variable)
- 여러 번 베르누이시행을 할 때 성공의 횟수 또는 실패의 횟수
표집된 단위 시간 또는 단위 공간 안에 특정 사건(드물게 발생)이 몇 번 발생할 것인지를 확률로 표현한 포아송 확률함수로부터 생성된 확률들의 패턴 또는 도수분포, 단위 시간 혹은 단위 공간 안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산확률분포
- : 포아송확률변수
- : 해당 사건의 발생수
- : 정해진 시간 안에 어떤 사건이 일어날 횟수에 대한 기댓값(모수), 평균발생횟수
- : 자연상수(2.71828...)
- 단위 시간당 사건 발생 횟수를 설명하는 분포 | 이항분포의 매개변수에서 n이 무한대로 가고 p가 작을 때 이항분포를 포아송 분포로 근사할 수 있음
- 어떤 집단에서 100세 이상까지 사는 사람들의 수
- 어떤 책 한 페이지에 있는 오타의 수
- 매일 잘못 걸려온 전화의 수
- 람다
- 어떤 일정 시간 또는 공간의 구간 안에서 발생한 평균 사건 수, 단위 시간이나 단위 면적당 사건이 발생하는 비율
첫 번째 성공(success)이 나올 때까지 독립적인 베르누이 시행을 할 때 나오는 확률분포, 기하확률함수로부터 나온 확률들의 패턴
k번째 성공이 나올 때까지 독립적인 베르누이 시행을 할 때 나오는 확률분포, 음이항확률함수로부터 나온 확률들의 패턴
- : 총 성공 횟수
- r=1일 때 기하분포가 됨
초기하확률함수가 생성한 확률들의 패턴
- 품질검사(불량 측정)
- N개의 공(흰 공 m개, 검은 공 N-m개)에서 비복원추출로 표본 n개를 뽑을 때 n개의 표본 중에서 흰 공의 개수가 나올 확률
지금까지 이산확률분포의 종류를 알아보았습니다. 이번에는 연속확률분포의 종류를 알아보겠습니다.
연속확률분포
균일분포
확률변수가 취하는 모든 구간에서 각 사건의 발생확률이 일정한 분포
- 두 균등분포의 합의 분포는 삼각확률밀도함수(triangular probability density function)로 만들어짐
정규분포와 표준정규분포
정규곡선(normal curve)으로부터 유래한 분포로 19세기 초 가우스(Carl F.Gauss)가 물리계측의 오차를 계산하는 과정에서 도입된 확률분포
- : 3.1416...(원주율[상수])
- : 2.7183...(자연대수[상수])
- : 분포의 평균
- : 분포의 표준편차
- 정규분포의 모양과 위치를 결정하는 것은 분포의 평균과 표준편차(분포의 평균(μ)과 표준편차(σ)를 제외하고는 모두 상수이고 X는 확률변수이기 때문)
- 정규분포의 확률밀도함수는 평균(μ)을 중심으로 좌우 대칭인 종모양을 이룸: 단봉분포(unimodal distribution)
- 확률변수 X가 취할 수 있는 값의 범위는 −∞ < X < +∞ 이므로 정규곡선은 X축(수평축)에 닿지 않음
- 분포의 평균(μ)과 표준편차(σ)가 어떤 값을 갖더라도, 곡선 아래의 면적은 모든 사건이 일어날 확률을 나타내므로 정규곡선 X축 사이의 전체 면적값은 항상 1
모수(평균, 표준편차)가 다른 정규분포를 가진 집단을 서로 비교하기 위해 정규분포를 표준화할 수 있습니다. 표본통계량이 '표본평균'일 때, 정규분포를 표준화(정규화)시킨 표본 분포를 표준정규분포(standard normal distribution)라고 합니다.
- 평균 = 0, 표준편차 = 1: 측정 단위에 영향을 받지 않게 중심위치와 척도 조정을 통해 절대 비교 가능
표준정규분포는 Z통계량으로 표준화시켰다고 해서 Z분포라고도 합니다. 표준정규분포는 개념적으로 정규분포와 동일하며 정규분포의 평균 해석에 많이 사용됩니다.
정규분포를 평균 μ=0이고 표준편차 σ=1 이 되도록 표준화한 분포, 표준정규확률함수가 생성한 확률 패턴
- 모집단이 정규분포를 이룰 때
- 표준화(standardization) 또는 정규화(normalization)한다는 의미는 평균을 빼고 표준편차로 나눈다는 뜻
- 어떤 확률변수 X의 관찰값이 그 분포의 평균으로부터 표준편차의 몇 배 정도나 떨어져있는가를 다음과 같이 표준화된 확률변수 Z로 나타냄
표준정규분포의 확률변수(확률밀도함수의 x축), 개별 데이터 포인트를 정규화한 결과
- 평균값에서 표준편차의 몇 배 정도 떨어져 있는지를 평가하는 수치
- 분자: 어떤 개별 데이터가 평균으로부터 떨어진 정도
- 분모: 해당 집단의 표준편차에 비해 떨어진 정도
- 표준편차의 ± 1배 범위 내: 약 68%
- 표준편차의 ± 2배 범위 내: 약 95%
- 표준편차의 ± 3배 범위 내: 약 99%
정규분포를 사용하여 이항분포의 확률을 구하는 방법
지수분포
포아송 분포에 의해 생성된 사건들 사이에 걸린 시간(interarrival time)에 대한 확률분포, 한 사건에서 그다음 사건까지의 시간이나 거리에 대한 도수분포
- : 단위 시간당(면적당) 발생하는 사건 평균 건수
- 정규분포 다음으로 일상생활의 문제를 잘 묘사할 수 있는 분포
- 감마 분포에서 α=1 인 분포
- 서로 독립인 지수확률변수들의 합의 분포는 감마분포를 따름
- 서비스 기관에서 두 고객이 도착했을 때 각 도착 사이의 시간
- 한 전자기기에서 특정 부품의 최초 고장과 다음번 고장이 일어날 때 걸리는 시간
지수분포를 일반화하면 감마분포(gamma distribution)가 됩니다.
감마분포
α번째 사건이 일어날 때까지(총 α번의 사건이 발생할 때까지) 걸리는 시간에 대한 확률분포
- : 팩토리얼(factorial) 함수를 실수와 복소수까지 확장한 함수, 팩토리얼의 범위를 복소수까지 넓혀 일반화한 함수
- : 형상모수(shape parameter)
- : 척도모수(rate/scale parameter)
- 감마분포는 지수분포의 합
- 지수분포를 일반화하면 감마분포가 됨: 감마분포의 α가 1이 되는 경우 지수분포가 됨 Gamma(1, λ) = Expotential(λ)
- 제2종 오일러 적분(Euler integral of the second kind)
베타분포
- 불순률
- 작동률
- 불량률
- 고장률
조건부 확률분포
일반화
적률/모멘트를 생성하는 함수
- MGF가 있으면 확률함수와 1:1 대응이 되며 각 MGF는 고유한 확률분포를 결정함(하나의 MGF는 하나의 확률분포로 대응함)
- 두 개의 확률변수가 동일한 MGF를 갖는다면, 두 확률변수는 동일한 확률분포를 갖게 됨
- 따라서, 확률변수에 대한 MGF를 찾는 것은 확률분포를 결정하는 것과 같음
- MGF를 미분하고 t=0을 넣으면 테일러급수(Taylor series)를 사용해 모멘트를 구할 수 있음: 1회 미분 시 첫 번째 모멘트 얻음, 2회 미분 시 두 번째 모멘트 얻음, ...
통계 기초
정의
표본을 이용하여 모집단의 특성을 파악하는 학문, 관심 또는 연구의 대상인 모집단의 특성을 파악하기 위해 모집단으로부터 일부의 자료(표본)를 수집하고 수집된 표본을 정리, 요약, 분석하여 표본의 특성을 파악한 후 표본의 특성을 이용하여 모집단의 특성을 추론하는 원리와 방법을 제공하는 체계, 학문
- 궁극적으로 알고 싶은 집단은 모집단임. 하지만 모집단은 정확히 알 수 없음. 따라서, 모집단에서 추출한 표본으로부터 모집단의 특성을 추정함
- 추정 결과를 검정하는 과정을 통해 최종적으로 모집단의 특성을 유추함
- 1단계 정의: 관심 또는 연구의 대상(문제, 주제, 가설) 설정
- 2단계 수집: 실험/관찰/조사를 통해 자료를 수집
- 3단계 분석: 수집한 자료를 정리, 요약, 탐색적으로 분석하여 자료의 특성을 파악
- 4단계 검증: 자료의 특성을 이용하여 관심 또는 연구 대상을 추론, 설정한 가설을 검증
분석 대상이 되는 집단의 특징을 측정한 데이터의 집합
- 데이터를 기반으로 불확실한 현실 세계에서 합리적인 의사결정을 돕는 도구
종류
일반
통계적 자료를 수집하고, 정리, 요약, 해석하는 과정을 통해 모집단 혹은 표본집단의 특성을 규명하는 통계학
- 수치(특성량)
- 표
- 그래프
표본에서 얻은 통계량을 기초로 해서 모집단의 특성을 추론하는 통계학
- 추정
- 검정
합리적 의사결정을 위해 통계적 방법론(도구 사용 등)에 입각하여 분석하는 통계학
- 분산분석
- 상관분석
- 회귀분석
- 다변량분석
모집단에 대한 가정 유무
모집단의 확률분포에 대한 명시적인 가정을 하는 통계학
- 대체로 수량적 자료(구간 자료, 비율 자료) 중에서도 연속적 자료가 사용됨
모집단의 분포모양에 대한 가정을 하지 않는 통계학
- 모집단의 분포모양에 대한 가정이 필요 없음
- 표본의 크기가 작아도 됨
- 주로 질적 자료(명목 자료, 서열 자료)를 사용
- 수량적 자료라 하더라도 빈도수와 같은 비연속적 자료를 많이 사용
통계적 추론에 대한 사고 방식
빈도론에 근거하여 통계적 추정, 가설검정, 분산분석 등의 방법
하나의 사건에서의 믿음의 정도(degree of belief)를 확률로 나타내는 베이즈 확률론에 기반한 통계학
- 경험에 따른 주관적 견해를 확률로 변환해서 추론에 이용
용어1: 모집단과 표본
우리는 다양한 정보를 알고 싶어 합니다. 예를 들면 다음과 같은 것들입니다:
- 대한민국 전체 인구의 삶의 만족도
- 특정 분야에서 일하는 모든 근로자의 평균 임금
- 어떤 공장에서 생산되는 모든 제품의 불량률
이처럼 연구, 조사, 또는 관심의 대상이 되는 전체 집단이나 데이터를 모집단(population)이라고 합니다.
연구/조사/관심의 대상이 되는 전체 집단/데이터
- 모집단을 구성하는 개체의 수가 유한한 모집단
- 로트(lot) 검사(제조단위번호가 있는 수입검사, 출하검사 등)
모집단을 구성하고 있는 구성 요소가 무한한 모집단
- 표본을 다시 복원하는 복원추출, 실험을 무한히 반복, 공정의 제조 능력(어느 공장에서 타이어를 만들고 있다고 할 때 공장의 생산능력은 연간 몇십만 본으로 규정되어 있어 유한모집단으로 생각되기 쉬우나 끊임없이 연료를 공급해서 타이어를 무한대로 생산할 수 있는 경우)
그러나 모집단 전체를 조사하는 것은 대부분의 경우 현실적으로 불가능하거나 매우 비효율적입니다. 시간, 비용, 인력 등 다양한 자원의 제약이 있기 때문입니다. 이러한 한계를 극복하기 위해, 우리는 모집단의 일부를 추출하여 그 특성을 조사합니다. 이렇게 추출된 모집단의 부분집합을 표본(sample)이라고 합니다.
연구자가 측정 또는 관찰한 결과들의 집합, 모집단으로부터 선택된 일부의 개체, 직접적인 조사 대상이 된 모집단의 일부, 모집단을 대표하여 추출틀로부터 뽑혀진 추출단위들의 집합
= 샘플같은 모집단에서 서로 영향을 주지 않으면서 동일한 확률로 추출된 표본
용어2: 데이터, 변수, 척도
정의
어떤 변수가 가질 수 있는 다양한 가능성 중의 하나가 현실 세계에 구체화된 값, 변수를 관찰하여 기록한 결과, 관찰/측정/실험 등을 통해 수집되며 의미를 갖을 수 있는 모든 사실 또는 값
= 자료요인(factor)을 구성하고 있는 요소(element)로 일정한 측정 단위(척도)로 표현될 수 있는 것, 자료분석의 관점에서 보는 자연 및 사회현상의 여러 가지 요인들, 연구자의 관심대상이 되는 성격 또는 속성(attribute)이나 연구대상들이 서로 구별되어 나타나는 속성, 데이터를 구성하는 모든 유형의 관측 기록을 아우르는 용어, 다른 상황에서 다른 값을 취할 수 있는 임의의 측정값, 다른 상황에서 다른 값을 취할 수 있는 임의의 측정값, 데이터를 구성하는 모든 유형의 관측 기록을 아우르는 용어
- 척도를 통해 측정할 수 있는 값 = 변할 수 있는 값
- 학생의 학업: 학업 성적(점) -
- 학생의 신체조건: 키(cm), 몸무게(kg), 혈액형(A, B, O, AB)
- 학생의 가정환경: 가족 구성원(부, 모, 형제/자매), 직업
대상 특성의 단위
종류
데이터는 완전히 분류되는 것이 아니라 상황에 따라 서로 중복될 수 있습니다.
기준1: 구조
미리 정해진 형식과 구조에 따라 저장된 데이터
- 가장 일반적인 형태는 행과 열이 있는 테이블 데이터(rectangular dada)
- 일반적으로 머신러닝 기법 활용
- 관계형 데이터베이스 테이블, 엑셀 스프레드시트, CSV(콤마로 구조가 결정됨)
구조화되어 있지만 데이터의 형식과 구조가 변경될 수 있는 데이터
- 스키마(데이터 개체, 속성, 관계와 이들에 대한 제약 조건들에 대한 정보) 수정이 쉽고 파일 단위로 구성되어 전송과 공유가 용이
- 정형 데이터와 비교하여 질의 처리(query processing)가 어려워 파일에 포함된 데이터 구조 정보를 바탕으로 데이터 분석에 사용할 경우 정형 데이터로 변환(테이블 형태의 데이터베이스 스키마로 변환)하고 데이터를 매핑(mapping)하여 정형 데이터로 변환할 수 있음
- HTML, XML, JSON
미리 정의된 구조가 없어 정형화되지 않은 데이터
- 반정형 또는 정형 데이터로 변환하는 전처리가 필요
- 딥러닝 기법 활용
- 텍스트(메일, 보고서, 소셜 미디어 게시물 등), 이미지, 음성, 동영상
기준2: 형식
테이블
행과 열로 이루어진 테이블 형태의 구조를 가진 데이터
- 이차원 행렬
- 엑셀 스프레드시트 테이블, 데이터베이스 테이블, 파이썬과 R의 데이터 프레임(data frame)
테이블의 각 행 @ 한 특정 경우에 대한 입력과 출력을 담고 있는 벡터
= 기록값, 사건(case), 개체/인스턴스(instance), 샘플(sample), 관측값/관측치(observed value), 관측개체, 사례/예제/예시(example), 패턴테이블의 각 열 @ 각 관측치의 특성치
- 연구에서 결과(outcome)을 예측하기 위해 열을 사용
- 피처벡터(feature vector)는 열에 있는 실제 데이터 모음을 의미
실험이나 연구에서는 결과(outcome)를 예측하기 위해 피처를 사용합니다. 이때 결과는 종속변수이고 피처는 독립변수입니다.
원인이 되는 변수, 어떤 변수가 다른 변수에 영향을 주고받는 경우 영향을 주는 변수, 응답치를 예측하기 위해 사용되는 변수
- 결과에 영향을 받지 않아 독립적이라고 함
- 표(table)에서는 원인이 되는 열을 의미
- 머신러닝에서는 데이터의 특징을 나타내는 변수를 의미함
결과가 되는 변수, 어떤 변수가 다른 변수에 영향을 주고받는 경우 영향을 받는 변수, 예측하고자 하는 변수, 연구자가 독립변수의 변화에 따라 어떻게 변하는지 알고 싶어하는 변수
- 원인에 종속받아 종속적이라고 함
- 표(table)에서는 결과가 되는 열을 의미
반응변수와 설명변수에 모두 영향을 미치는 변수
- 위약효과(placebo effect), 관찰자 편향(observer bias)
비테이블
- 동일한 개체에 대해 횡단면 자료와 시계열 자료가 합쳐진 것
하나의 변수를 여러 시점에서 관측한 자료
- 시간의 경과에 따른 추세를 알고 싶을 때
- 동일한 변수 안에 연속적인 측정값을 갖음
- 관중 추이, 주가, 현금흐름
서로 다른 개체에 대해 매 시점에서 조사된 시계열 자료(pseudo panel)
- 동일한 걔체를 반복적으로 관찰하는 것이 아님
- 물리적 관계, 사회적 관계, 추상적이 ㄴ관계 표현
기준3: 측정
정형 데이터는 측정 가능 여부에 따라 수치형 데이터(numerical data)와 범주형 데이터(categorical data)로 나뉩니다.
수치형 데이터
수치로 표현되며 수학적 연산이 의미 있는 측정 가능한 데이터, 양적 변수를 기록한 자료
- 수치 자료를 범주화하면 순서자료가 됨
- 수치형 데이터 X: 우편번호
속성을 수치로 나타낼 수 있는 변수
수치형 데이터는 연속성 여부에 따라 이산형 데이터(discrete data)와 연속형 데이터(continuous data)로 나뉩니다.
셀 수 있는(countable) 형태의 자료, 정수 데이터, 이산변수의 관찰 결과
- 범주형 자료의 발생빈도를 표현하기도 함
- 자녀의 수, 주사위 눈의 수, 책의 페이지 수, 학급의 학생 수, 일별 방문자 수, 사건 발생 빈도
정숫값을 취할 수 있는 변수
- 각 세대의 자녀수, 자동차의 판매대수
연속적인 수로 표현하는 자료, 실수 데이터, 연속적 변수의 관찰 결과
- 데이터 자체를 숫자로 표현
- 대부분 이산화를 통해 절사된 형태로 표시
- 연속형 데이터를 순서형 데이터로 표현하면 정보의 손실이 발생함
- 몸무게, 키, 나이, 수입
연속적인 모든 실숫값을 취할 수 있는 변수
- 길이, 무게, 온도 변화
범주형 데이터
수학적 연산이 불가능하거나 의미 없으며 가능한 범주 안의 값만을 취하는 데이터, 질적 변수를 기록한 자료
- 범위가 정해진 값을 갖음
- 1) 전혀 다른 집합: 사과, 오렌지, 2) 정도를 나타내는 요인변수의 수준(낮음, 중간, 높음), 3) 구간별로 나뉜 수치 데이터
둘 이상의 배타적 개별 범주로 구분되는 측정값을 갖는 변수
속성을 수치로 나타낼 수 없는 변수
= 정성변수범주형 데이터는 순서를 매길 수 있는지 여부에 따라 명목형 데이터(이진형 데이터 포함)와 순서형 데이터로 나뉩니다.
대상의 범주적 속성만을 나타내는 질적 자료
- 숫자를 바꾸어도 값이 크고 작음을 나타내는 것이 아니라 단순히 범주를 표시하는 것
- 국적, 성별, 결혼상태(기혼/미혼), 혈액형, 도시명, 우편번호, TV 스크린 종류(플라즈마/LCD/LED), 제품 불량 여부(양품/불량), 보험/신용카드 사기 여부(정상/비정상), 고객 이탈 여부(유지/이탈), 이메일 스팸 여부(정상/스팸)
측정 대상의 특성을 분류 또는 구분하기 위하여 숫자를 부여하는 변수
- 가장 낮은 수준의 변수
- 수준: 범주
- 성별, 국적, 인종, 종교, 거주 지역, 우편번호, 자녀 유무, 혈액형, 운동선수 등번호, 질병여부, 자동차 색깔, 수술한 병원
숫자로 표현될 수 있지만 수량적인 의미를 갖지 않고, 범주를 구분하는 용도로 쓰이는 척도
- 각 자료를 구분하는 용도로만 사용하는 척도
- 말 그대로 명목적인(이름뿐인) 단위
특정 사건의 발생 유무와 같이 두 가지 값(0/1 또는 참/거짓)만을 갖는 범주형 데이터
- 이진 데이터의 집합은 어떤 사건이 발생한 경우의 수 또는 백분율로 요약할 수 있음
- 암 수술 후 사망 여부를 나타내는 데이터(1=생존, 0=사망), 제품불량여부(양품/불량), 보험사기여부(정상/비정상)
0또는 1만 가지는 변수, 예/아니오라는 두 가지 값으로만 대답할 수 있는 질문과 같은 변수
= 더미변수(dummy variable), 지표변수(indicator variable), 설계변수(design variable), 처치(treatment), 이진지시자(Boolean indicator)대상의 속성을 순서로 구분할 수 있는 범주형 데이터, 순위를 매길 수 있는 데이터
- 상대적 비교 가능
- 범주화를 통해 수치자료를 순서자료로 바꾸기도 함
- 순서 자료에서 명목 자료가 되면 정보의 손실이 발생함
- 학력, 학년, 학점, 계급, 메달, 평점(1~5), 비만도, 선호도
측정 대상 간의 순서를 매기기 위하여 사용되는 변수
- 명목변수보다 한 단계 높은 수준의 변수
- 수준: 범주 + 순위
- 석차, 등급, 등수, 성적, 학력, 군인의 계급, 경제적 수준, 선호도, 만족도, 신뢰도
관찰 대상의 순위를 나타내는 척도
- 서열은 있지만 간격이 서로 같지 않으므로, 수량화할 수 없고 사칙연산 불가능
측정대상의 순서뿐만 아니라 순서 사이의 간격을 알 수 있는 변수
- 수준: 범주 + 순위 + 등간
- 섭씨 온도, 지능지수, 대학학년
관측 대상이 지닌 속성의 차이를 양적인 차이로 측정하기 위하여 척도 간 간격을 균일하게 분할하여 측정하는 척도
- 관측 대상의 속성을 정량적으로 측정 및 사칙 연산 수행, 비교 가능
등간변수의 특성에 더하여 측정자료 간의 비율계산이 가능한 변수
- 수준: 범주 + 순위 + 등간 + 절대영점
- 연령, 무게, 시간, 거리
서열성, 등간성, 비율성, 절대 영점의 속성을 모두 가진 척도
- 절대 영점이 있는 등간 척도
기준5: 변량수
하나의 변수만 있는 자료
= 일변량 데이터, 단변량 데이터두 개의 변수로 이루어진 자료
= 이변량 데이터여러 개의 변수로 이루어진 자료
= 다변량 데이터기준6: 집단
구성원이 변하지 않는 특정한 모집단으로부터 얻어진 자료
- 2022년 출생아
기준7: 수집 목적
조사자가 직접 수집한 자료
- 조사 목적에 맞게 측정 도구를 설계하고 개발할 수 있기에, 목적에 가장 부합되는 자료들을 수집할 수 있음
- 설문지(대인면접법, 전화면접법, 우편조사법, 인터넷조사법 등으로 수집됨)
당면한 조사목적이 아닌 다른 목적을 위해 수집되고 정리되어 있는 자료로 직, 간접적으로 조사목적에 도움을 줄 수 있는 자료
- 자료의 원래 목적이 조사자의 목적과 다를 수 있으므로 자료의 활용 가능성, 적합성, 신뢰성 등에 대한 사전 평가가 매우 중요
- 정부간행물, 연구보고서, 사내자료
기준8: 머신러닝
모델 f(X) 구축 시 사용되는 데이터
= 학습 데이터구축된 모델을 검증하는데 사용되는 데이터
기타
연구자 또는 관찰자가 관심을 갖는 대상, 연구 대상
- 학생
개체의 특성 중에서 연구자가 특별히 관심을 갖는 특성
- 학생의 학업, 신체조건, 가정환경
통계적 준비
자료 수집
방법
자료를 얻는 방법에는 실험(experiment), 관측(observation), 조사(survey)가 있습니다.
가설이나 이론이 실제로 들어맞는지를 확인하기 위해 연구자가 실험참가자를 임의로 다양한 조건하에 배치하여 설명변수와 반응변수 사이의 인과성(casuality)을 조사하는 일
- 어떤 조작을 가해 그에 따라 일어나는 변화를 조사하고 결론을 내는 일
- 코로나(covid19) 백신이 실제로 효용이 있는가?
실험과 달리 어떤 조작을 가하지 않고 연구자가 자료의 생성과정에 전혀 관여하지 않으면서 설명변수와 반응변수의 연관성(association)을 밝히는 일
- 표본에 영향을 미치지 않으면서 표본의 개체들을 측정하거나 조사
- 큰 의미에서 측정(measurement)을 포함
- 절차: 분석 문제 결정 -> 대상 선정 -> 관심 속성 결정 -> 척도 설정 -> 측정 -> 데이터셋 생성
- 1) 분석 문제 결정: 반려동물 제품 회사에서 강아지 옷을 제작하려고 한다. 고객의 신체 사이즈를 정확히 모르는 상태에서 어떤 사이즈의 신제품을 만들어야 하는가?
- 2) 대상 선정: 신체 사이즈에 대한 조사가 가능한 강아지들로 이루어진 여러 개의 표본을 구성한 뒤, 특정 표본과 해당 표본의 구성원을 무작위로 선정
- 3) 관심 속성 결정: 성별, 목둘레, 가슴둘레 등
- 4) 척도 설정: 남/여, cm, inch 등
- 5) 측정
- 6) 데이터셋 생성
실험이나 관찰/측정을 통하여 데이터를 획득할 수 없는 경우에 데이터를 얻는 방법
- 설문지나 조사지 등을 통해 데이터를 얻음
- 여론조사, 의식조사
전향적 연구(prospective study)는 실험연구와 관측연구에서 모두 사용합니다. 반면 후향적 연구(retrospective study)는 주로 관측연구에서 사용됩니다.
연구자가 대상자를 추적 관찰하면서 정보를 얻는 연구
- 실험과 관측연구 모두에서 사용
- 질환 발생 여부를 연구하기 위해 연구대상자의 비만 정도를 위험군과 일반군으로 나눈 다음 일정 기간 이후 두 그룹간의 질병 발병률을 비교
이미 일어난 일에 대한 정보를 얻는 연구
- 주로 관측연구에서 사용
- 폐암 환자들을 대상으로 과거 흡연 여부를 알아보는 연구
실험
실험에 대한 계획을 의미하는 것으로 해결하고자 하는 문제에 대하여 자료를 수집하기 전에 실험 실시 방법, 데이터 취득 방법, 표본 크기 결정, 공간이나 시간의 배치법, 통계적 방법 등을 파악하여 어떤 환경에서 데이터를 분석하면 최소의 실험 횟수로 최대의 정보를 얻을 수 있는가를 계획하고, 최적의 작업(생산)조건을 결정하는 것을 다루는 학문
- 최소의 실험횟수로 최대의 정보를 획득
- 실험의 계획뿐만 아니라 실험을 통한 자료의 분석까지도 포함
- PPDAC(Problem - Plan - Data - Analysis - Conclusion)
특성치에 영향을 준다고 생각되는 무수히 많은 원인들 중에서 실험(관측값)에 영향을 줄 수 있는 원인/속성/변수
= 요인실험에서 데이터의 형태로 측정되는 결과치
= 반응치, 반응변수(response variable)실험을 하기 위한 인자의 여러 가지 조건, 각 인자가 취할 수 있는 값들의 그룹/범위/종류
= 요인 수준, 인자 수준(factor level), 조건서로다른 여러 인자 및 수준이 있을 때 이 인자와 수준들의 조합, 여러 인자 및 수준의 서로다른 조합에 따라 다양하게 실험하는 행위
= 처치자연과학의 실험에서 세운 가설을 검증하기 위해 실험 조건을 통제하여 실험을 수행하는 대상 집단
자연과학의 실험에서 실험군에 대해 실험 조건을 실험 전 상태에서 변동시키지 않고 그대로 두어 실험군의 결과와 자연 상태를 대조해 보기 위해 만드는 집단
관측
측정 도구로 측정하여 얻은 값, 측정 도구의 표준단위가 몇 개인가를 수치로 나타낸 것
- 변수들이 측정을 통해 실현된 값
- 관측값/측정값은 참값의 근삿값임
- 길이, 들이, 무게, 넓이, 부피, 질량, 온도, 시간
실제수, 양에 대한 실제 값
- 측정한 대상물의 실제 값, 어떤 사람이 측정하든 모두 같은 값을 낼 수 있는 것
- 학생수, 은행에 예금한 돈의 액수
어림수
측정값들로 구할 수 있는 참값에 가장 가까운 추정값
- 참값을 대신하는 값으로 사용됨
조사
관심의 대상이 되는 집단을 이루는 모든 개체들을 조사하여 모집단의 특성을 측정하는 통계조사 방법
- 자원(인력, 예산 등)이 많이 필요함
- 물리적 한계로 현실적으로 불가능한 경우가 많기 때문에 대부분 표본조사를 이용함
- 인구주택총조사
- 농림어업총조사
- 조선(대한제국포함)시대 27명 임금의 수명 자료
관심의 대상이 되는 전체 모집단 중 일부(표본)를 선택하고 그 선택된 일부만을 대상으로 조사를 실시하여 이로부터 전체 모집단의 특성을 추정하는 통계조사 방법
- 전수조사에 비해 자원이 절감되고 조사 결과를 신속하게 얻을 수 있으며 심도 있는 조사가 가능함
- 단, 모집단에서 추출한 소수의 표본이 전체 모집단의 특성을 잘 대표해야 일반화의 오류가 발생하지 않음
- 절차: 표본조사의 목표 설정 -> 모집단의 정의 -> 추출틀과 추출단위의 결정 -> 표본추출방법 선정 -> 현지조사 -> 데이터 분석 및 보고서 작성
자료 추출
정의
모집단에서 일부 표본을 뽑아내는 과정
- 데이터 편향을 최소화하기 위한 방법
- 모집단을 효과적으로 잘 나타내는 올바른 표본을 선택해야 함
- 핵심 질문1: 표본추출의 대상(모집단)은 무엇인가?
- 핵심 질문2: 몇 개(명)의 표본을 어떻게 뽑을 것인가? - 표본 크기 및 표본추출 방법
- 핵심 질문3: 조사된 표본자료는 어떻게 분석할 것인가?
- 핵심 질문4: 추출된 표본이 모집단을 대표할 수 있는가? - 대표성(representation)
종류
모집단에 속해 있는 각 구성원이 표본으로 선택될 가능성이 일정하게 되도록 하는 표본추출방법, 모집단에 속하는 모든 추출단위에 대해 사전에 일정한 추출확률이 주어지는 표본추출법
- 특정한 표본이 선정될 확률을 토대로 추정오차를 과학적으로 설명할 수 있음
- 모집단을 대표할 수 있는 표본을 뽑는 유일한 방법
확률과는 상관없이 연구자가 모집단과 비슷하다고 생각되는 표본을 임의로 추출해 내는 방법, 특정 표본이 선정될 확률을 알 수 없는 표본추출법, 각 추출단위들이 표본에 추출될 확률을 객관적으로 나타낼 수 없는 표본추출법
- 확률표본추출(무작위추출)이 불가능하거나 비경제적일 때
- 장점: 확률표본추출에 비해 간편하고 경제적
- 단점: 추론결과의 정확도(precision)을 알 수 없음, 오차 추정 불가능
확률표본추출
모집단 내의 선택 가능한 원소들을 무작위로 추출하는 방법, 크기가 N인 모집단에서 크기가 n인 표본을 무작위로 추출하는 방법
- 실제 대규모 조사에서는 거의 사용되지 않지만 다른 표본추출법의 기초가 됨
- 각 추첨에서 모든 원소는 동일한 확률로 뽑힘
- 모집단의 모든 구성원의 성격이 서로 비슷하고, 분석도 단일성격에 대한 것일 때 더욱 효과적
- 모집단 층화 없이 임의표본추출을 통해 얻은 표본을 단순임의표본(simple random sample)이라고 함
- 유의미한 비임의 방식으로 표본이 추출되지 않으면 표본편향이 생김
- 컴퓨터로 추출
- 난수표
모딥단에 번호를 부여하고 일정한 n개의 간격으로 표본을 추출하는 방법, 표집틀에서 처음 1~k번째 단위들 중 하나를 랜덤하게 선택한 다음, 매 k 간격으로 단위들을 표본으로 추출하는 방법
- 표집틀이 없어 고유번호를 부여할 수 없는 등 단순확률추출법을 적용하기 어려운 실제 조사현장에서 폭넓게 사용
- N/n 또는 정확도 고려해서 추출간격 k를 결정한 뒤 1~k 에서 난수 하나를 선택해서 시작점을 선정하고, 시작점에 k를 반복적으로 더해서 표본추출
- 모든 표본이 선택될 확률은 동일
- 모집단 크기 = 500 이고 표본크기 = 50 일 때, 1~10 사이에서 특정 번째(3, 13, 23, ..., 493) 대상자 선정해서 50개의 표본을 얻음
- 어느 잡지사가 구독자의 의견을 묻고 싶을 때, 구독자카드에 번호를 붙인 다음, 매 10번째 또는 매 100번째 구독자를 표본으로 하여 질문하는 것
- 선거출구조사: 선거 당일 출구에서 투표를 하고 나오는 유권자의 숫자를 세어 특정 번째(1, 11, 21, 31, 41 번째 등)의 유권자를 대상으로 조사를 하는 경우
- 주차장 출입 차량에 대한 조사
표본을 뽑기 전에 모집단을 성격에 따라 서로 중복되지 않는 여러 개의 층(strata)으로 나누고, 각 층에서 단순확률추출 방법으로 표본을 추출하는 방법
- 부모집단(subpopulation)의 구성 내역을 알고 있음
- 층의 구성(성별, 연령, 지역 등)
- 종교의 분포를 파악하려는 경우에 전체모집단을 연령별, 성별, 지역별로 구분한 다음, 각 집단별로 무작위추출을 하는 것
- 총원이 10000명인 대학교에서 1000명을 추출할 때, 단과 대학별로 구분지은 다음 다시 학과별 구성에 맞춰 표본 추출
- 서울시내 서점의 월 매출액을 추정하기 위해 100개의 서점을 대형, 중형, 소형으로 분류한 후 각 층에서 일정 수의 표본을 추출
각 층에서의 표본의 사례수, 즉 표본크기를 정할 때 모집단에서 각 층이 차지하는 구성비율을 고려해서 표본을 추출하는 방법
- 총원이 10000명인 대학교에서 1, 2, 3, 4학년의 비율을 4:3:2:1로 유지하면서 총 1000명을 추출하려고 할 때 학년별로 400, 300, 200,100명씩 추출하여 1000명의 표본을 구성
표본을 뽑을 때 직접 개별적인 구성원을 선택하는 것이 아니라 자연적 또는 인위적인 집단을 먼저 뽑고 그 집단 중에서 필요한 만큼의 표본을 추출하는 방법, 서로 인접한 조사단위들을 묶어 구성한 집락(cluster)을 추출하고 이들 집락 내의 조사단위들을 조사하는 방법
- 조사단위에 대한 표집틀 확보는 어렵지만 상대적으로 집락에 대한 표집틀 확보는 쉬운 경우
- 단계별로 정보를 얻을 수 있는 경우
- 조사단위들이 산재되어 있어 관측비용이 많이 드는 경우(어떤 특정 지역에서 집중적으로 표본을 뽑음)
- 서울시내 초등학교 3학년 학생들의 평균 지능을 알기 원할 때 개별적인 학생을 구성원으로 삼는 것이 아니라, 학교단위 또는 학급단위를 구성원으로 간주하여 그중에서 무작위로 몇 개의 학교를 뽑거나 몇 개의 학급들을 뽑는 방법
- 서울시 고등학생의 월평균 사교육비를 추정하고 싶을 때 서울시에 있는 모든 고등학교가 있는 리스트(확보하기 쉬움)에서 고등학교 몇 개를 무작위로 추출하여 추출한 고등학교(primary sampling unit, PSU)에서 다시 학급을 뽑고 해당 학급에서 학생을 추출
- 계층(stratum)
- 공통된 특징을 가진 모집단의 동종 하위 그룹
- 단순임의표본(simple random sample)/단순랜덤표본
- 모집단 층화 없이 임의표본추출로 얻은 표본
비확률표본추출
모집단에서 연구자가 가장 손쉽게 구할 수 있는 구성원을 선택하여 표본으로 삼는 표본추출방법, 응답자를 선정하는 데 있어 조사원 개인의 자의적인 판단에 따라 간편한 방법으로 표본을 추출하는 방법
- 자발적 참여(백화점 앞에서 설문지 돌리는 것, 도심지에서 지나가는 사람들을 대상으로 면접조사, 포털사이트 인터넷 조사, TV 프로그램의 자동응답장치 ARS를 이용하는 여론조사)
- 어떤 수업방법의 효율성을 알아보기 위하여 직접 중학교 학생들에게 그 방법을 실험하려고 할 때, 연구자의 모교를 선택하여 실험하는 것
조사자가 자기의 지식과 경험에 의해 모집단을 가장 잘 대표한다고 여겨지는 표본을 주관적으로 선정하는 방법
- 모집단의 성격이 매우 이질적이거나, 여러 가지 사정으로 인하여 표본의 크기가 아주 작은 경우
- 단점: 조사자의 주관적 판단에 의해 표본이 추출되기 때문에 그 표본을 통해 얻은 추정치의 정확성에 대해 객관적으로 평가할 수 없음
- 전문가 선택(어느 교육연구소의 연구원이 전체 학생들의 평균성적을 알아보기 위해 전체 학생들의 성적을 대표한다고 생각되는 몇 학교를 나름대로 선택하는 경우)
- 물가의 변동을 대표하는 소비자물가지수를 계산할 때 모집단을 이루는 수많은 상품 중에서 물가변동을 잘 반영하는 몇 개의 품목만을 표본으로 삼아 계산하는 것
연구 대상이 되는 모집단의 계층과 계층이 차지하는 비율을 사전에 파악하여 비례대로 표본을 선정하는 방법, 조사목적과 밀접하게 관련되어 있는 조사대상자의 연령이나 성별과 같은 변수 값에 따라 모집단을 부분집단으로 구분하고 모집단의 부분집단별 구성비유과 표본의 부분집단별 구성비율이 유사하도록 표본을 선정하는 방법
- 단기간에 조사를 해야하는 경우
- 장점: 비용이 적게 들고 쉬움
- 단점: 그룹 내 조사대상 선택에서 랜덤화 과정 없음, 경우에 따라서 심각한 오차 발생
- 어느 대학에서 학생 서비스 만족도를 조사할 때 기존의 자료를 바탕으로 학과별, 학년별, 성별 구성비율을 알아본 다음 그 비율에 따라 표본을 학과별, 성별로 할당하는 방법
재표본추출
관측 데이터로부터 반복해서 표본추출하는 과정
- 부트스트랩과 순열(셔플링) 과정을 포함
현재 있는 표본에서 추가적으로 표본을 복원추출하고 각 표본에 대한 통계량과 모델을 다시 계산하는 것
- 원래 표본을 수천, 수백만 번 복제하는 것
- 이를 통해 원래 표본으로부터 얻어지는 모든 정보를 포함하는 가상 모집단을 얻고, 이 가상 모집단으로부터 표본분포를 추정할 목적으로 표본을 수집함
- 통계량이나 모델 파라미터(모수)의 표본분포를 추정하는 쉽고 효과적인 방법
- 데이터나 표본통계량이 정규분포를 따라야 한다는 가정이 꼭 필요하지 않음
관측 데이터 집합으로부터 얻은 복원추출 표본
오차
일반적으로 참값과의 차이를 일컫는 용어
- +오차와 -오차는 같은 빈도로 발생
- 매우 큰 오차는 거의 발생하지 않음
- 작은 오차는 큰 오차보다 자주 발생
모집단을 대표할 수 있는 전형적인 구성요소를 표본으로 선택하지 못했기 때문에 발생하는 오류
- 요인1: 표본의 크기 때문에 생기는 우연에 의한 오류
- 요인2: 편의 때문에 발생하는 오류로 모집단을 대표할 수 없는 비전형적인 구성요소를 표본으로 뽑았기 때문에 일어나는 오류
표본의 선택방법과는 관계없이 주로 표본의 특성값을 측정하는 방법이 부정확하기 때문에 발생하는 측정오차가 주류를 이루는 오류
- 한 사람에게 두 사람이 같은 질문을 하였지만, 서로 다른 대답을 얻는 경우(집문하는 사람의 질문방법, 설명부족 등이 원인)
- 설문지를 통해 개개인의 특성 및 태도를 조사 또는 분석할 때에도 연구에 따라 설문지의 결과에 차이가 발생하는 경우(설문지에 대압하는 사람의 개인적인 반응양식 작용)
- 연구가 어떤 목적에 사용되는가를 조사대상자에게 알렸을 때 오히려 부적확한 반응을 얻는 경우(생활수준을 알기 위해 학생들에게 보호자의 월수입을 물을 때에는 조금 과장하여 대답할 가능성이 있음, 장학금 대상자를 선발하기 위하여 질문을 할 때에는 실제보다 낮은 수준으로 대답할 가능성 있음)
물리량의 측정에 따라 수반되는 오차
- 과대오차
- 계통오차
- 우연오차
측정오차는 과대오차(mistake, blunder), 정오차(constant error), 우연오차(random error)로 나누어집니다.
관측자의 과실, 부주의, 기술의 미숙으로 인해 발생하는 오차
- 정오차와 우연오차보다 크기가 상대적으로 매우 커서 쉽게 발견되고 측정값에 큰 영향을 줌
- 오차 제거 가능
- 기록 및 계산의 착오, 눈금 읽기의 착오, 측침의 이동, 측정 횟수의 오차
오차의 발생 원인이 분명하고 오차의 발생 방향과 크기가 일정하여 수식에 의해 보정이 가능한 오차
- 측정을 되풀이하면 이 오차가 쌓여서 커짐(정오차는 측정횟수에 비례)
- 노력으로 제거 가능
- 측정의 정확도와 관련있음
- 기계오차/장비오차(instrumental error): 측정에 사용되는 관측 기계의 불완전성(기계의 구조적 특성, 불완전한 조정 등)으로 인해 발생하는 오차
- 자연오차/환경오차(natural error): 관측 시 자연 현상과 환경 조건의 변화(바람, 습도, 중력, 온도 등)로 측정을 방해받음으로써 발생하는 오차
- 개인오차(personal error): 관측자의 숙련도나 관측 습관(최소눈금 읽는 방법, 측량기계의 수평 맞추기 등) 등에 의해 발생하는 오차
오차 발생 원인이 분명하지 않고 과대오차를 제거하고 정오차를 보정하고 나서도 남아있는 오차, 실험측정을 반복할 때 측정값들의 변동성으로 인해 발생하는 불가피한 오차
- 원인을 밝힐 수 없음
- 항상 발생하며 제거 불가능
- 측정에 수반된 우연한 현상에 대해서 확률/통계적 접근이 필요
- 측정의 정밀도와 관련있음
용어
필요한 정보를 얻기 위해 조사를 할 때 조사의 대상이 되는 가장 최소의 요소
= 단위(unit)모집단에서 표본을 추출하기 위해 설정한 기본단위들의 집합
- 하나의 기본단위 또는 여러 개의 기본단위로 구성
- 중복 또는 누락되어서는 안 됨
표본이 실제로 추출되는 추출단위의 목록
= 표집틀, 추출틀모집단에서 표본이 선택된 비율
- 모집단 = {a, b, c, d, e} 에서 2개의 표본을 추출한다고 할 때 어떤 게체가 표본으로 뽑힐 확률은 2/5
모집단이 다른 특성을 가지는 부모집단들로 이루어진 경우, 부모집단의 구성비율과 표본의 구성비율이 다르면 전체 모집단에 대해 왜곡된 결과가 나오는 것을 방지하기 위해 곱해주는 수치
- 한 개의 표본이 몇 개를 대표하는지를 나타내는지를 뜻함
- 층별확률추출법에서는 확률추출에 대한 가중치, 무응답에 따른 가중치, 사후충화를 위한 가중치를 곱해서 최종 가중치를 만듬
관심의 대상이 되는 모든 기본단위들의 집합
- 일반적으로 말하는 모집단과 같은 개념
- 조사시점, 지리적 경계, 연령 기준 등 시공간상 명확하게 정의됨
- 수도권 거주 초등학생 학부모 대상 조사
현실적인 제약을 고려해서 조사 가능하고 추출틀을 작성할 수 있는 추출단위만을 모아서 만든 모집단, 표본추출틀을 통해 추출될 수 있는 기본단위들의 집합
- 전화여론조사: 전화번호 목록(표본추출틀)에 등재된 전화보유 가구의 성인
척도
참값에 근접한 정도, 개별 측정값이 실제값/진실값/참값/기준값에 일치하는/차이나는 정도, 측정하거나 계산된 양이 실제값과 얼만큼 가까운지를 나타내는 기준
- 편의성(bias)이 작음을 의미
- 계통오차가 적은 정도를 나타내는 개념
- 개별 탄착점이 기준점과 차이가 크면 정확도가 낮다고 함
측정의 재현성, 동일 유형으로 반복 측정한 측정값들의 분포(퍼짐 정도), 측정치 분포가 넓거나 좁거나 하는 정도, 측정값의 퍼짐이 좁은 정도
- 낮은 정밀도: 재현성/반복성이 좋지 않음(측정마다 단일 값에 수렴하지 않고 매번 다른 값이 나타남)
- 높은 정밀도: 재현성/반복성이 좋음, 낮은 랜덤오차(산포 작음), 측정 데이터 간 적은 오차
- 우연오차가 적은 정도를 나타내는 개념
- 통계적 변동성의 척도
- 탄착군이 작게 형성되면(분포가 조밀하면) 정밀도가 높다고 함
통계적 기술
자료 정리
자료가 간단할 때는 표만으로도 변수 간의 관계를 파악할 수 있습니다. 하지만 자료의 양이 많아지면 좀 더 직관적인 방법이 필요합니다. 이때 사용할 수 있는 방법이 그래프(graph)입니다.
수집된 자료나 결과를 보다 시각적으로 쉽게 이해시키고 일목요연하게 표현하는 그림
- 자료의 경향성 분석 및 파악
- 자료속에 존재하는 집단간의 차이 여부 확인
- 변수간의 연관성 파악
- Cleveland(1985)에 따르면 차이에 대한 인지 순서는 다음과 같음: 동일한 척도에서의 위치, 길이, 각도와 기울기, 면적, 부피, 색상, 밀도 순
그래프는 자료의 특성을 한눈에 파악할 수 있어 효과적입니다. 하지만 그래프는 보는 사람에 따라 다르게 해석될 여지도 있습니다. 그래서 실제로 자료를 분석할 때 최종 결과는 객관적으로 비교할 수 있는 자료의 요약 수치를 함께 제시합니다. 이처럼 자료를 표와 또는 그래프를 이용해 시각화하고, 수치를 요약하면서 자료의 특성을 파악해나가는 과정을 탐색적 자료 분석이라고 합니다.
탐색적 자료 분석은 변량의 수와 자료의 속성에 따라 목적이 다르며 자료별로 방법을 다르게 적용합니다. 자료별 분석목적과 정리하는 방법은 다음과 같습니다.
공통
표
특정 구간(interval = 빈(bin))에 속하는 자료의 개수를 나타내는 표, 각 범주에 몇 개의 관측 개체가 있는지를 정리한 표, 수집된 자료를 적절한 등급(class) 또는 범주(category)로 분류하고 각 등급에 해당하는 빈도수 등을 정리한 표
- 자료의 특성을 요약하고 정리하는 기술적 통계학에서 가장 기본적인 역할을 수행
- x축에 변숫값들을 y축에 횟수를 표시
용어
각 구간에 해당하는 관찰된 수, 빈도수, 절대도수(absolute frequency)
= 빈도각 범주에 속하는 빈도수가 전체관찰수(n)에 비해 차지하는 값
상대도수에 100을 곱해 표준화한 값
어떤 등급에 해당되는 빈도를 포함해서 그 이하 또는 그 이상에 있는 모든 빈도를 합한 것
= 누적빈도한 집단에서 어떤 등급 이상 또는 이하에 해당되는 누적빈도가 전체관찰대상 중 차지하는 비율
= 상대누적도수, 누적비율양적 자료에서 숫자 범주로 나눈 관찰값, 몇 개의 관찰값을 하나의 범주로 묶은 것
- 계급의 수는 자료의 특성을 고려해 분석자가 결정
등급의 간격
- 구간 = 5.0
연속적 자료를 등급으로 묶을 때 관찰값이 포함되어 있는 정확한 범위
- 체중(X)가 ...35~39, 40~44, 45~49...로 나누어져 있다면 정확한계는 39.5~44.5
하한계(lower limit)와 상한계(upper limit)의 중간에 해당하는 수치, 등급의 대푯값
일변량 범주형 자료
단변량 범주형 자료는 범주형 변수 1개에 대한 자료입니다. 단변량 범주형 자료에 대해서는 관측값의 수를 세는 빈도 분석을 진행합니다.
그래프
일변량 범주형 자료를 시각화하는데는 막대그래프와 파이 차트를 사용합니다.
각 범주의 빈도수 혹은 비율을 막대로 나타낸 그림 @ 표현값에 비례하는 높이를 지닌 직사각형 막대로 범주형 데이터를 표현하는 차트나 그래프
- 비교하고 싶을 때
- 축이 0에서 시작하면 차이를 구분하기 힘들기 때문에 특정 틀(긍정적, 부정적)에 편향되지 않는 선에서 차이를 잘 보여줄 수 있는 '논리적이고 의미 있는 기준선'부터 막대그래프를 보여주기도 함
- 수직 막대 차트(vertical bar chart)
- 수평 막대 차트(horizontal bar chart): 동일한 특성에 따른 순위를 매길 때 가장 유용
- 단순 누적 막대 차트(simple stacked bar chart)
- 100% 누적 막대 차트(100% stacked bar chart)
막대를 최고에서 최저 빈도 순으로 정렬한 막대그래프에 누적 빈도에 대한 선이 추가된 막대그래프
= 파레토도원에 각 범주에 해당되는 비율만큼 각도를 분할하여 표시한 그림, 각 범주의 빈도수 혹은 비율을 원의 부채꼴 모양으로 나타낸 그림
- 전체에서 차지하는 비중을 보여주고 싶을 때
- 원을 사용하는 이유는 각 범주의 각도와 면적의 비가 항상 동일하기 때문
- 비교를 목적으로 한다면 막대그래프를 사용
일변량 수치형 자료
일변량 수치형 자료는 변량이 1개이며 변량의 속성이 수치형인 데이터입니다.
표
일변량 수치형 자료는 일변량 범주형 자료와 마찬가지로 도수분포표로 표현할 수 있습니다. 일변량 수치형 자료를 도수분포포로 나타내려면 범주화를 해야합니다. 수치형 자료를 범주화하면 순서형 자료로 변환됩니다.
그래프
각 관측값의 위치에 점을 표시하고 같은 관측값이 있는 경우 위로 누적한 그림, 데이터들의 분포를 점으로 나타내주는 도표
- 자료를 흐트려서(jittering) 데이터 포인트들이 서로 겹치지 않게 보이게 하는 시각적 효과를 줄 수 있음
가공하지 않은 자료 그대로를 이용하여 그린 것이 아니라, 자료로부터 얻어낸 통계량인 5가지 요약 수치(최솟값, 제 1사분위, 제 2사분위, 제 3사분위, 최댓값)를 가지고 그린 그래프
- 자료의 주요 위치 파악
- 이상점 검출
- 수치자료 분포의 산포를 나타냄
- 주로 분포들을 서로 비교하기 위해 사용됨
상자그림에서 최솟값
= min whisker상자그림에서 최댓값
= max whisker표본분포가 특정 분포에 얼마나 가까운지를 보여주는 그림
도수 분포표를 막대그래프로 나타낸 것, x축은 구간들을 y축은 빈도수를 나타내는 도수 테이블의 그림
- 수치자료 중에서도 특히 연속자료의 분포형태를 나타냄
- 계급의 상대도수를 사각형의 면적으로 표시: 전체 면적 = 1
- 막대도표에서 X축은 각 요인변수(factored variable)의 서로 다른 범주들을 나타내고 Y축은 도수 또는 상대도수를 나타냄
- 반면, 히스토그램의 X축은 수치적으로 나타낼 수 있는 하나의 변수 값을 나타내고 Y축(높이)은 밀도를 나타냄
- 히스토그램에서 최빈값(mode)은 가장 길이가 높은 막대의 양 끝 지점을 해당 막대의 양 옆 막대의 끝지점을 사선으로 교차시킨 교차점
- 변수가 연속적이라는 것을 보여주기 위해서 각 등급의 막대가 붙어 있음
여러 차례 반복적으로 관측한 합의 자료를 구간별로 분류하고 구간별 도수를 계산한 뒤 도수를 밀도단위로 바꾸어 밀도단위 히스토그램으로 나타낸 것
상자의 내용물 및 추출횟수로부터 합이 각각의 값으로 실현될 확률을 계산하여 이를 그래프로 나타낸 것
측정된 스케일로 이루어진 데이터를 연속적인 간격으로 나누고 각 간격에서 관측되는 표본의 빈도를 카운트하여, 그값을 막대의 높이로 하여 데이터의 밀도를 표현한 것
히스토그램은 구간 간격에 따라 모양이 달라진다는 단점이 있습니다. 이를 보완한 것이 밀도 그림(density plot)입니다.
히스토그램을 부드러운 곡선으로 나타낸 그림
- 밀도는 얼마나 모여있는지를 높이로 표시한 것
- y축 값의 단위는 개수(히스토그램)가 아닌 x축의 두 점 사이에 있는 분포의 비율
- 밀도 곡선 아래의 총 면적은 1
- 주로 커널밀도추정(kernel density estimation)을 사용
어떤 변수가 가질 수 있는 값 및 그 값을 가질 가능성의 정도를 추정하는 것, 데이터로부터 변수가 가질 수 있는 모든 값의 밀도(확률)을 추정하는 것, 어떤 변수의 확률밀도함수를 추정하는 것
특정한 종류의 분포를 따른다는 가정하에 확률밀도함수를 추정하는 방법
- 확률변수가 정규분포를 따른다고 가정하면 관측 데이터로부터 평균과 분산을 구하면 됨
확률밀도함수를 추정할 때 함수의 형태에 대한 가정(assumptions) 없이 주어진 자료로부터 직접 확률밀도함수를 추정하는 방법
- 히스토그램(histogram)
- 커널 방법(kernel method)
- 직교열 방법(orthogonal series method)
- 최근접 이웃 방법(nearest neighbor method)
- 벌점 가능도(penalized likelihood)
- 다항 스플라인 모형(polynomial spline)
- 가변 커널(variable kernel)
- 사영 추적(projection pursuit)
- : 확률변수
- : 데이터
- : 데이터 갯수
- : 커널함수
- : 커널함수의 대역폭 또는 평활 매개변수(smoothing parameter)
관측값의 정보를 그대로 간직하면서 자료의 분포를 알려주는 그림
- 전체적인 분포의 형태는 파악하는 히스토그램에서 개별적인 데이터 정보가 사라지는 단점을 보완함
도수 분포를 나타내는 막대그래프에서, 직사각형의 윗변 중점을 잡고 도수가 0인 계급을 하나식 추가하여 차례로 선분으로 연결하여 이루어지는 꺾은선그래프의 일종. 도수분포를 꺾은 선 그래프의 형태로 도수의 변화량을 표시하여 다각형 모양으로 표현한 것
- 같은 변수에 대한 여러 가지의 경우를 분석할 때 유용(히스토그램의 경우 여러 그래프를 겹쳐 그리면 지저분해지기 마련인데, 데이터가 다각형 형태로 나타나 비교가 용이)
- 도수분포다각형의 계급을 점차 줄여 도수를 많이 취할수록 다각형 모양의 그래프는 점차 곡선이 되어 가는데 이때 생기는 곡선이 도수분포곡선
- 분포다각형의 선과 x축이 이루는 도형의 넓이는 막대그래프의 막대들의 넓이의 합과 같음
도수분포표의 각 등급구간에서 누적백분율만큼 올라가서 점을 찍고 각 점을 연결한 것
= cumulative percentage curve, 누적백분율곡선다변량 범주형 자료
다변량 범주형 자료는 범주형 변수가 2개 이상인 자료입니다. 다변량 범주형 자료는 명목형 변수 사이의 빈도를 교차분석하여 정리합니다.
표
두 개 이상의 변수를 동시에 고려하여 각각의 범주에 관측개체의 빈도를 정리한 교차표
- 칸(cell): 각 범주에 교차되는 부분
- 분석목적에 따라 비율을 다르게 표시함
- 수치자료를 범주화해서 순서자료로 만든 후 분할표를 작성할 수도 있음
- 성별과 혈액형 간의 관계
- 세 가지 스마트폰 모델에 대한 성별 선호도
- 탑승객별 타이타닉호 생존률
k개 범주형 변수에 대한 분할표
- 3차원 분할표: 타이타닉호 생존자와 사망자 수를 조사 시 변수는 생존여부, 성별(어린이), 객실등급(승무원)
그래프
변량이 모두 범주형인 다변량 범주형 데이터를 시각화 할 때는 다중 막대그래프와 누적 막대그래프를 이용할 수 있습니다. 이밖에도 모자이크 그래프(mosaic plot)를 이용할 수도 있습니다.
그룹 내의 데이터 백분율을 보여주는 누적 막대 그래프, 분할표를 시각화한 그래프
다변량 혼합 자료
다변량 혼합 자료는 데이터를 그룹 또는 범주로 나눈 분류자료와 수치자료가 혼합된 자료 유형입니다. 정당별 지지율, 성별/지역별 인구수 등은 모두 혼합 자료유형에 속합니다. 다변량 분석에서 혼합 자료를 분석하는 목적은 그룹 간 비교입니다. 범주에 따라 나뉜 그룹들 간에 얼마나 차이가 있는지 없는지를 비교하는 것입니다. 다변량 혼합 자료는 표와 그래프로 정리할 수 있습니다.
표
혼합 자료를 표로 정리할 때는 그룹별 표본의 크기와 평균, 표준편차, 최댓값, 최솟값을 표기하면 됩니다.
그래프
혼합 자료를 시각화 할 때는 그룹별로 점도표, 히스토그램 또는 막대그래프를 만들어서 만든 그래프를 중첩하거나 병렬로 놓아 그룹 간의 차이를 비교하면 됩니다. 또 동일 축 상에 놓여있는 그룹별 상자그림을 서로 비교할 수도 있습니다.
여러 개의 변수를 병렬적으로 배열하여 모든 데이터 포인트를 비교하는 선그래프
= parallel coordinates다변량 수치형 자료
다변량 수치형 자료는 수치자료로만 이루어진 자료 유형입니다. 다변량 수치형 자료를 분석하는 목적은 수치 변수들 간의 관계를 유도하는 것입니다. 수치 변수들이 선형관계인지 아닌지를 파악하는 것입니다. 다변량 수치형 자료의 경우에는 표를 그리기 보다 그래프를 이용해서 자료를 정리합니다.
그래프
다변량 수치형 자료를 그래프로 표현할 때는 일변량 수치형 자료를 시각화하는 모든 그래프를 이용할 수 있습니다. 여기에 더해 다음과 같은 그래프를 추가로 그릴 수 있습니다.
순서쌍 자료를 2차원 평면상에 점으로 표시한 그림
- 두 수치변수 간에 관계가 있는지를 시각적으로 확인하고 싶을 때
- x, y축은 각각의 변수들을 의미
- 그래프의 각 점은 하나의 레코드를 의미
- 각각의 관측개체에 대해 두 변수의 값을 순서쌍으로 표시
3개 이상의 수치변수에 대해 두 변수씩 쌍으로 조합하여 산점도를 행렬형태로 표시한 것
- 2002년 1월부터 2010년 12월까지 우리나라 전체의 월간 평균기온, 강수량, 평균습도 간의 관계 조사
각 변수 쌍의 선형 관계 정도를 측정하는 상관 계수 값(상관도)을 사각형 셀 행렬로 표시한 그림
= 상관행렬, 상관매트릭스각 등급구간의 중간점에 해당되는 점 위에서 그 등급의 빈도수에 점을 찍어 그 점들을 이어서 나타낸 그래프
- 시간 경과에 따른 연속적 데이터의 변화 추이를 나타낼 때
- 연속적 자료에서만 사용
- 질적 자료나 이산적 자료에서는 사용할 수 없음
- 경제지표(환율, 주가지수 등)가 시간에 따라 변하는 양상
시간에 따라 수집된 자료를 이용해서 x축에 관측시점, y축에 관측된 값을 표시한 산점도
- 자료 간 종속성이 있어 관측순서가 중요
- 순서 파악을 쉽게하기 위해 일반적으로 관측 순으로 관측값들을 선으로 연결
- Gapminder 참조
- 1990년부터 2020년까지의 올림픽 육상 100m 우승기록
- 2010년부터 2022년까지 월별 하루 평균출생아수
시간 경과에 따라 수량의 변화를 표시하는 그래프
- 시간 경과에 따른 연속적 데이터의 변화 추이와 각 번주가 차지하는 비율의 변화를 보고 싶을 때
지금까지 범주형 자료와 수치형 자료를 표와 그래프로 정리하는 방법을 알아보았습니다. 정리한 자료에 자료의 특성을 요약한 수치를 더해주면 자료를 정확하게 파악할 수 있습니다.
자료 요약
자료를 요약하는 방법은 자료의 속성에 따라 달라집니다. 범주형 자료는 각 범주의 빈도(frequency)로 요약합니다. 각 범주에 해당하는 빈도가 자료의 요약값입니다. 다변량 범주형 자료는 각 범주의 도수를 이용해 그룹별로 비교할 수 있습니다.
반면, 수치형 자료는 위치(location), 산포(dispersion), 형태(shape)에 따라 자료를 요약합니다. 이 기준으로 자료를 기술하는 방법을 각각 위치통계(location statistics), 산포통계(dispersion statistics), 비대칭통계(asymmetry statistics)라고 합니다. 각 분야에서 사용하는 요약값은 다음과 같습니다.
- 위치통계: 평균(mean), 중앙값(median), 최빈값(mode)
- 산포통계: 범위(range), 분위수(quantile), 변동(variation), 분산(variance), 표준편차(standard deviation), 변동계수(coefficient of variation)
- 비대칭통계: 왜도(skewness), 첨도(kurtosis)
다변량 수치형 자료도 위 요약값들을 이용해 그룹별로 비교할 수 있습니다. 여기에 더해 다변량 수치형 자료는 두 변수 간의 관계를 공분산(covariance)와 상관계수(correlation coefficient)로 요약할 수 있습니다.
- 공분산(covariance)
- 상관계수(correlation coefficient)
그럼 각 방법을 차례로 살펴보겠습니다.
위치 통계량(중심 경향성): 일차 모멘트
위치 통계량은 데이터의 중심 위치를 나타냅니다. 이들은 데이터의 중심 경향성 측도(measures of central tendency)입니다.
관찰된 자료가 어느 위치에 집중되어 있는가를 나타내는 값
전체 데이터셋의 주요 특성을 간단히 요약하는 수치
- 평균, 중앙값, 최빈값, 분산, 표준편차, 분위수 등
최빈값
가장 쉽게 구할 수 있는 대푯값(typical value)은 최빈값(mode)입니다. 최빈값은 데이터에서 가장 자주 나타나는 값입니다. 최빈값은 범주형 데이터를 이해하는데 적합합니다.
자료 중 빈도가 가장 많은 값
- 가장 자주 보이는 값이 무엇인지 알고 싶을 때
- 질적 자료와 이산적 자료의 분포에서 빈도수가 어느 곳에 가장 많이 모여 있는가를 보여줌
- 여러 개가 나올 수 있다는 단점이 있음
- 연속자료의 경우 값들이 매우 세분화되어 있어 최빈값이 없을 수도 있음
- 범주형 데이터에서 사용하며 수치형 데이터에서는 잘 사용하지 않음
- 가장 많은 고객들이 원하는 물건을 찾고 싶을 때
연속적 자료를 등급으로 묶어서 각 등급에 해당되는 빈도수를 적을 때 빈도수가 많은 등급
- 연속적 자료의 분포에서 빈도수가 가장 높은 등급이 어느 곳에 가장 많이 모여 있는가를 보여줌
- 100개 타이어의 수명을 등급으로 나누었을 때 타이어 수명의 최빈등급은 빈도수가 가장 높은 등급, 최빈값은 해당 등급의 중간점
하지만 최빈값은 연속형 데이터에서 사용이 제한적입니다. 여러 개의 최빈값이 존재할 수 있어 대푯값으로서의 안정성도 떨어집니다. 이때는 다른 중심 경향 척도인 평균(mean)을 사용할 수 있습니다.
평균
모든 값의 총합을 전체 자료의 개수로 나눈 값, 합의 평균
- 하나의 온전한 데이터 집합의 총체적 영향력을 측정하고 싶을 때
- : 각 등급의 빈도
- : 해당 등급의 중간점
- : 전체등급수
- : 모집단에서 얻은 표본의 개수
- 무게중심을 의미
- 모든 자료의 정보를 이용함
- 추론통계에서 가장 중요한 집중화경향값으로 사용됨
- 단, 데이터 집합에 속한 모든 값들이 계산에 포함되기 때문에 데이터 집합에 관련성이 떨어지는 특이값들이 있으면 대표성을 상실할 수 있음
각 항의 수치에 그 중요도에 비례하는 계수를 곱한 다음 산출한 평균, 가중치를 곱한 값의 총합을 가중치의 총합으로 나눈 값
- 자료값이 가지는 중요성이 다를 때
- : k개 집단의 전체평균
- : 각 집단의 관찰수
- : 각 집단 관찰수에 대응하는 평균
- 기댓값이기도 함(가중치는 해당 확률)
- 교락 요인(confounder)을 통제하는 데 사용
단, 평균은 극단값(outlier)에 민감하여 전체 데이터의 특성을 왜곡할 수 있습니다.
대부분의 관측값으로부터 멀리 떨어져 있는 일부 관측값
= 특잇값, 이상점극단값들에 민감하지 않다는 것을 의미
= resistant절사평균과 중앙값
중앙값(median)과 절사평균(trimmed mean)을 사용할 수도 있습니다. 이 두 통계량은 모두 로버스트(robust)합니다. 로버스트하다는 것은 극단값들에 민감하지 않다는 것을 의미합니다.
수치로 된 자료(양적 자료)를 크기 순서대로 나열할 때 데이터에서 가장 가운데에 위치한 값
- 값의 순서를 매기고 싶을 때
- : 중앙값이 있는 구간의 정확하한계
- : L까지의 누적빈도
- : 중앙값이 있는 구간의 빈도
- : 관찰수
- : 구간의 크기
- 평균과 중앙값이 비슷하면 정보를 많이 활용한 평균 사용
- 데이터 집합 내의 특이값들의 영향을 받지 않음
- 표본평균에 비해 로버스트하지만 자료의 정보를 다 활용하지 못함
- 주택 가격
- 소득 수준
데이터를 오름차순으로 정렬한 후 어떤 위치를 기준으로 상위 절반의 가중치의 합이 하위 절반의 가중치의 합과 동일한 위치의 값
- 누적 가중치가 전체 가중치 합의 50%를 초과하는 첫 번째 데이터 포인트를 가중중간값으로 선택
- 중간값과 마찬가지로 특잇값에 로버스트함
정해진 개수의 극단값을 제외한 나머지 값들의 평균
- : 전체 관측수
- : 작은 것과 큰 것의 수
- α% 표본절사평균 = 순서통계량에서 하위 α%부터 상위 α%까지의 자료를 이용하여 표본평균을 계산
- 표본평균과 표본중앙값의 장점만 취함
- 체조, 피겨스케이팅, 다이빙 대회 채점
- 최솟값, 최댓값 제외
기타
곱의 평균
- 평균수익률
- 연간 총소득의 연평균 증가율
역수의 산술평균의 역수
- 평균속력
평균은 가장 중요한 대푯값이지만 중앙값과 최빈값을 무시한 평균은 대푯값이 될 수 없습니다. 따라서 항상 전체 그림을 보면서 가장 적절한 대푯값을 선택하는 것이 바람직합니다.
변이 통계량(산포도): 이차 모멘트
데이터를 파악하는 두 번째 방법은 데이터가 중심으로부터 얼마나 밀집해 있는지 또는 퍼져 있는지를 알아보는 산포도(dispersion)을 파악하는 일입니다.
자료들이 얼마나 퍼져 있는지를 나타내는 측도, 관찰된 자료가 흩어져 있는 정도
- 중심위치가 얼마나 안정적인지에 대한 중요한 정보를 제공: 자료가 조밀하게 모여있다면 중심위치의 변동성이 작아지고, 자료가 넓게 퍼져 있다면 중심위치의 변동성이 커짐
데이터의 분산도를 나타내는 측도에는 편차(deviation), 분산(variance), 표준편차(standard deviation), 범위(range), 사분위범위(interquantile range, IQR), 변동계수(coeffcient of variation)가 있습니다.
차이를 이용하는 방법
편차
개별 자료(데이터, 변량, 관측값)와 전체 자료의 평균값과의 차이, 관측값과 위치 추정값 사이의 차이
- 개별 자료가 평균으로부터 얼마만큼 떨어져 있는가를 나타냄
- 기술통계학에서의 오차
편차의 절댓값
각 데이터 값과 평균 간의 절대 차이의 평균, 편차의 절댓값의 평균
- : 표본평균
중간값으로 구한 절대편차들의 중간값
- 각 값의 절댓값의 중앙값에서 x의 중앙값을 빼서 계산
- 로버스트함
분산 및 표준편차
절대편차 대신 제곱편차를 이용하는 분산과 표준편차도 있습니다.
제곱편차의 평균, 편차의 제곱합을 평균화한 값, 평균과의 편차를 제곱한 값들의 합을 n-1로 나눈 값
- : 데이터 개수
- 변동을 평균화시킨 개념
- 차이의 제곱의 합으로 표현된 측도
- 평균을 빼면 위치에 영향을 받지 않음
- 표본을 가지고 모집단을 추정하는데 표본 평균을 구해서 표본 분산을 구하기 때문에 그 파라미터 개수인 1개를 빼서 자유도(파라미터 예측에 필요한 독립 정보의 수)를 n-1로 설정
편차의 제곱합, 제곱 편차들을 합한 값
2개의 모집단에서 추출된 표본 간의 분산이 같음
2개의 모집단에서 추출된 표본 간의 분산이 다름
표준편차는 분산보다 데이터를 더 정확하게 해석합니다. 원본 데이터와 같은 척도(scale)에 있기 때문입니다.
분산에 제곱근(root)을 취한 값, 분산의 제곱근
분산과 표준편차는 분산도를 측정할 때 가장 보편적으로 사용하는 방법이지만 모두 특잇값에 민감합니다.
순서를 이용하는 방법
차이 대신 순서를 이용할 수도 있습니다.
정렬된 데이터를 나타내는 통계량
- 데이터의 최솟값부터 최댓값까지 정렬된 데이터 값에 따른 계량형
범위
가장 기본이 되는 측도는 범위(range)입니다.
데이터의 최댓값과 최솟값의 차이
- 최댓값과 최솟값에만 영향을 받기 때문에 자료 전체의 퍼져 있는 정도를 파악할 수는 없음
하지만 범위는 특잇값에 매우 민감합니다. 범위에서 특잇값을 제외하면 변이를 측정하는 유용한 척도가 되는데 이것이 분위수입니다.
분위수
데이터를 크기 순으로 나열했을 때, 전체 데이터를 특정 비율로 나누는 값
- 백분위수(percentile)
- 십분위수(decile): 10, 20, ..., 90번째 백분위수
- 사분위수(quartile): 25, 50, 70번째 백분위수
P번째 분위수는 데이터를 100등분하여 전체 데이터의 P%를 아래에 두는 값, 하위 P%에 해당하는 값, 어떤 값들의 P퍼센트가 이 값 혹은 더 작은 값을 갖고 (100-P)퍼센트가 이 값 혹은 더 큰 값을 갖도록 하는 값
= 분위수자료를 동일한 비율로 4등분 할 때의 세 위치
- : 전체 관측수
75번째 백분위수와 25번째 백분위수 사이의 차이, 제3사분위수와 제1사분위수의 차이
- L보다 작거나 U보다 큰 값은 이상점
- 상자그림에 나타냄
기타
평균으로 표준편차를 보정한 값
- 표준편차가 평균에 영향을 받아 표준편차만 이용하여 산포를 비교하는 것이 적절하지 않은 경우
- 100을 곱해 표본평균에 비해 표본표준편차가 얼마나 큰지를 % 개념으로 표시하기도 함
비대칭 통계량: 삼차/사차 모멘트
왜도(skewness)와 첨도(kurtosis)는 자료의 분포 형태에 대한 측도입니다. 많은 통계분석 방법에서는 모집단이 중심위치를 기준으로 대칭(symmetric)을 이룬다는 가정합니다. 이 두 척도는 모집단의 대칭성 가정을 얼마나 만족하는지를 확인하는데 사용합니다.
자료가 대칭적으로 분포되어 있는지 아니면 한쪽으로 기울어져 있는지에 대한 측도
- 좌우가 대칭이라면 음수와 양수가 상쇄되어 왜도는 0 근처
- 평균에서 멀어질수록 왜도는 큰 음수나 큰 양수가 됨
- 두터운 꼬리(heavy tail): 꼬리가 길게 분포
- 오른쪽 꼬리가 김: 큰 양수값을 가짐 = 양의 왜도(positive skewness), skewed to the right
- 왼쪽 꼬리가 김: 큰 음수값을 가짐 = 음의 왜도(negative skewness), skewed to the left
- 고르지 않은 소득 분배
- 큰 손실을 입을 낮은 가능성
산술평균과 중앙값의 차이가 표준편차에 비하여 얼마나 떨어져 있는가를 나타내는 것
- : 피어슨의 비대칭도
- : 표준편차
- : 중앙값
- 양(+)의 값: 오른쪽 꼬리분포
- 음(-)의 값: 왼쪽 꼬리분포
양쪽꼬리가 얼마나 두터운지를 나타내는 값
- 이상점(극단적인 사건의 발생 등)의 유무를 알고 싶을 때
심한 왜도나 첨도를 가지는 경우 자료에 이상점이 있을 가능성이 높아집니다.
통계적 추론
정의
표본 데이터를 바탕으로 모집단의 특성을 추정하고 결론을 도출하는 과정이 바로 통계적 추론(statistical inference)입니다.
이미 알고 있는 사실이나 명제를 토대로 결론을 이끌어 내는 사고 과정
- 논리적 추론(연역적 추론, 귀납적 추론)
- 통계적 추론
표본을 통해 모집단의 특성을 추측하는 통계학의 핵심 과정, 제한된 데이터를 바탕으로 더 큰 집단에 대한 결론을 도출
- 모집단에 대한 미지의 특성을 파악하는 것
종류
통계적 추론은 크게 세 가지 유형으로 나뉩니다.
모집단의 분포가 특정한 확률분포를 따른다고 가정하고 이루어지는 추론 방법
- t-검정, F-검정, 분산분석(ANOVA) 등
모집단의 분포에 대한 특정 가정 없이 이루어지는 추론 방법
- Mann-Whitney U 검정, Wilcoxon 부호 순위 검정 등
사전 확률과 관찰된 데이터를 결합하여 모수의 사후 확률 분포를 추론하는 방법
- 베이즈 정리를 기반으로 하며, 사전 분포와 우도 함수를 사용
통계적 추론은 크게 다음과 같은 단계를 거칩니다.
- 표본 추출: 모집단에서 대표성 있는 표본을 선택합니다.
- 통계량(summary statistics) 계산: 표본으로부터 통계량(평균, 분산, 표준 편차 등)을 계산합니다.
- 추정(estimation): 표본 통계량을 사용하여 모집단 모수의 값(점추정)이나 범위(구간추정)를 추정합니다.
- 가설 검정(hypothesis testing): 모집단에 대한 가설을 설정하고 검증합니다.
- 결론 도출: 분석 결과를 바탕으로 모집단에 대한 결론을 내립니다.
1단계: 통계량 계산
통계적 추론의 두 번째 단계는 통계량(statistic) 계산입니다.
정의
통계량은 모수(population parameter)를 추론하기 위해 표본으로부터 계산된 함수입니다. 예를 들어, 표본 평균(x̄)이나 표본 분산(s²)이 통계량에 해당합니다. 모수는 모집단의 특성을 수치로 나타낸 것입니다. 예를 들어, 모집단의 평균(μ)이나 분산(σ²)이 여기에 해당합니다.
표본들로 구성된 함수, 표본을 조사하여 얻은 데이터를 가지고 모수를 추정하기 위해 만든 공식, 모수에 대한 점추정량, 더 큰 모집단에서 추출된 표본 데이터들로부터 얻은 측정 지표, 반복해서 표본을 얻었을 때 각 반복마다 표본 통계치들이 나타내는 통계량, 단 하나의 수로 대상이되는 자료 집단(확률 모델) 특성을 잘 설명할 수 있는 값/변수/특성량, 표본의 특성을 수치화하는 측도
- 대표값: 통계량은 자료 집단의 특성을 잘 설명
- 모수 추정: 모집단의 특성인 모수를 추정하는 데 사용
- 가설 검정: 특수한 통계량은 통계적 검정을 위해 사용됨(검정통계량)
- 통계량은 매 표본마다 무작위로 변하는 확률변수로 간주(모집단으로부터 동일 크기로 취해지는 기회 표본은 무한히 많고 표본이 추출될 때마다 각 표본의 통계량은 일정하지 않기 때문)
- 표본을 뽑을 때마다 통계량의 값이 달라지는 표본추출변동 문제가 있음
- 표본 평균
- 표본 분산
- 표본 비율
- 표본 분산들의 비율
모집단의 특성을 나타내는 수치, 관심을 갖고 있는 조사변수에 대한 모집단 전체의 특성치(parameter), 모집단의 특성을 수치로 나타낸 것, 확률분포의 모양을 결정하는 값
- 연구자가 실제로 알고싶어 하는 것은 모집단 데이터가 아니라 모집단의 특성을 설명하는 모수
- 모수는 모집단이 변하지 않기 때문에 값이 변하지 않음
- 1개 집단 비교: 모평균, 모분산, 모표준편차, 모비율
- 2개 집단 비교: 모평균의 차이, 모비율의 차이 모분산의 비율
- 모평균: 평균소득, 평균신장
- 모비율: 찬성률, 지지율
- 모총계: 우리나라 전체 경지면적, 총사교육비
종류
통계량의 종류에는 대표적으로 표본 평균, 표본 분산, 표본 비율 등이 있습니다.
표본 평균
모집단의 산술평균
- : N개의 사례수로 구성된 동일 모집단에서 뽑은 서로 독립적인 관찰치(i.i.d.)
- : 모집단의 관찰수
표본 추출 때마다 구해지는 각 표본의 평균, 모집단의 단일 표본 하나의 평균
- : N개로 구성된 모집단에서 n개의 표본을 뽑았을 때 표본의 관찰값(i.i.d.)
- : 매 표본 추출 때 마다 취하는 표본의 수/크기
표본 분산
모집단의 각 관찰값과 평균과의 편차를 제곱하여 그 평균을 구한 것
- 관찰값들 간의 차이가 클수록 커짐
표본들이 나타내는 표본분포 상에서의 분산, 표본의 각 관찰값과 표본 평균과의 편차를 제곱하여 그 평균을 구한 것, 표본평균들의 분산
- : 자유도(degree of freedom)
- 표본분산은 모분산의 불편추정량(unbiased estimator)
- 표본분산을 만들 때 표본의 총 개수 n이 아니라 n-1로 나누면 편향을 줄일 수 있음(편차의 합 = 0이라는 제약조건 때문에 n-1개의 편차 정보를 사용)
- 표본분산은 편차의 제곱합을 이용하기 때문에 분산의 단위도 관측값 단위의 제곱이 됨
모집단의 표준편차
표본의 표준편차
표본 비율
모집단 전체에서 어떤 특정 속성을 갖는 대상 수의 비율
어떤 성질을 갖는 요소가 표본에서 차지하는 비율, 표본의 비율
- 표본비율은 표본 평균
- 여론조사 정당 지지율, 방송사 시청률
두 개 숫자의 상대적 크기를 비교한 것, 단순히, a : b 또는 a/b 와 같이, 두 수를 비교/대비시키는 것
- 분자와 분모가 서로 독립적인 관계로 서로 다른 범주일 때 사용
- 성비, 인구밀도(인구/면적)
전체 또는 기준량과 비교/대비시켜 수치화한 것, 비의 특수한 형태로 분모에 분자가 포함
- 전체 지원자 중 경력 지원자의 비율: 경력 지원자/(신입 지원자+경력 지원자)
특정기간 동안에 발생된 사건을 그 사건의 위험에 노출된 총 횟수(건수, 사람수)로 나눈 것
- 보통 천분율(‰)로 표현
- 이혼의 빈도를 나타내는 지표로서 1년 동안의 이혼건수를 그 해 중간시점의 인구로 나누어 천분비로 산출한 조이혼율
분포
중요한 점은 통계량이 확률변수라는 것입니다. 통계량이 값이 변할 가능성이 있는 확률적 성격을 띈다는 것입니다. 무작위 표본을 여러 번 추출하면 그때마다 다른 값이 나오며 이것은 확률입니다. 표본의 변화에 따라 값이 변하는 통계량은 확률변수입니다. 즉, 확률변수로서 통계량은 함수이며, 각 확률변수에 대응하는 확률분포를 가집니다. 통계량을 확률변수로 취할 때 나타나는 이 확률분포를 표집분포(sampling distribution)라고 합니다. 통계량은 확률변수, 확률함수와 더불어 통계학에서 가장 중요한 3개의 함수입니다.
연구 대상이 되는 전체 집합의 확률분포
통계량의 확률분포, 동일한 모집단에서 같은 크기의 표본을 반복적으로 추출할 때, 특정 통계량의 값들이 따르는 분포, 실제로 얻을 수 있는 모집단 분포나 표본 분포와 달리 통계적 추론을 위해 무수히 많은 기회 표본 집단에 대해 표본통계량(매 표본 통계치들이 나타내는 통계량)을 확률변수로 취하는 이론적인 확률 분포, 표본통계량을 확률변수로 취할 때 나타내는 확률분포, 모집단에서 추출된 대상군의 확률분포, 모집모집단에서 일정한 크기로 뽑을 수 있는 표본을 모두 뽑았을 때 그 모든 표본의 특성치(통계량의 확률분포), 하나의 동일한 모집단에서 얻은 여러 샘플에 대한 표본통계량의 도수분포, 여러 표본들 혹은 재표본들로부터 얻은 표본통계량의 도수분포
- 표본의 변동성(sampling variability)을 나타냄
- 표본통계량의 도수분포는 계산된 지표의 값이 표본마다 다르게 나타날 수 있음
- 확률 계산이 목적이 아니라 통계적 추론(추정, 가설검정), 분산분석 시 사용됨
- 어떤 데이터 집합에서의 개별 값(데이터 포인트)의 분포를 의미하는 데이터 분포(data distribution)와는 다름
가장 잘 알려진 표집분포의 예는 표본 평균의 표집분포입니다.
표본 평균의 표집분포
표본 평균들의 표준편차
- : 표본값들의 표준편차
- : 표본크기
- 매번 뽑히는 여러 표본 평균들이 얼마만큼의 변동, 즉 편차를 가지는지를 알려주는 지표
- 표준편차? 편차(변량-평균) 제곱의 평균의 제곱근, 표준오차? (추정값-참값)의 제곱의 평균의 제곱근
- 표본이 참값인 모평균에서 얼마나 떨어져있는지를 알려줌
- 표준오차가 작다? 뽑힌 표본 평균들 간의 편차가 작다 = 표본 평균들이 모평균과 큰 차이가 나지 않는다 = 뽑핀 표본집단들로 모집단을 추정하기에 적합하다
- 표본 크기: 표본의 크기가 커질수록 표준오차는 작아짐 (이때 표본분포는 모분포보다 더 위로 솟고 좁은 종모양이 되고 모평균 주위로 표본평균들이 모임)
- 비례성: 표준 오차는 표본 크기 n의 제곱근에 역비례(모집단 표준편차를 n제곱근으로 나눈 값과 같아짐), n 제곱근의 법칙(square-root of n rule) 즉, 표준오차와 표본 크기 사이의 제곱근 관계에 따라 표준오차를 2배로 줄이려면 표본 크기를 4배 증가시켜야 함
- 정확성: 표준오차가 작아질수록 통계량과 모수 간의 편차도 작아짐. 결과적으로 표본평균에 의한 모수 추정이 정확해짐
표본평균의 표집분포의 모양은 어떨까요?
모집단이 정규분포일 때
어떤 모집단의 평균이 이고 분산이 인 정규분포를 이루고 해당 모집단으로부터 크기가 n개인 표본들을 독립 추출했을 때, 표본의 평균들이 이루는 표집분포는 평균이 이고 분산이 인 정규분포를 이룹니다.
특정한 모집단에서 동일한 크기로 가능한 모든 표본을 뽑아서 각각의 표본들의 평균을 계산했을 때 그 평균들의 확률분포, 선택가능한 모든 표본들로부터 계산된 표본평균들의 확률분포, 모집단에서 표본 크기가 n인 표본을 여러 번 반복해서 추출했을 때 각각의 표본 평균들이 이루는 분포
- 모집단의 크기가 매우 크거나 무한하거나 모집단이 작더라도 복원추출함
- 모집단이 정규분포를 이룸
- 표본의 각 관측값(확률변수)은 동일 모집단에서 추출되었으며 서로 독립적임(identically independent distribution, i.i.d.)
- 평균의 표집분포는 표본의 크기 n에 관계없이 언제나 정규분포를 이룸
- 표본 평균의 표본 분포는 모집단 분포보다 변동성이 작아짐(매 표본 평균이 나름의 중심위치를 나타내는 대표값이기 때문)
- 표본 평균은 모평균을 추정/검정하는데 바람직한 성질들을 갖기 때문에 모평균의 추정량, 검정통계량에 표본 평균을 사용함
- 정규화하면 표본평균의 확률분포는 표준정규분포를 따름
또한, 2개의 모집단이 모두 정규분포를 따를 때 두 모집단으로부터 나온 표본 평균 차이의 분포도 정규분포를 이룹니다.
2개의 모집단이 정규분포를 따를 때 각 모집단에서 뽑은 표본의 평균 차이의 분포
- 2개의 모집단이 정규분포를 따를 때 각 모집단에서 뽑은 표본평균의 차이는 정규분포를 따름
모집단이 비정규분포일 때
모집단이 정규분포가 아니더라도 추출할 표본의 크기가 충분히 크면() 평균이 이고 분산이 인 임의의 모집단에서 추출한 표본들()의 평균의 표집분포는 중심극한정리(central limit theorem)에 따라 정규분포 $$N(\mu, \dfrac{\sigma^2}{n})$$에 근사하게 됩니다.
모집단이 평균이 μ, 표준편차가 σ인 임의의 분포를 이룬다고 할 때 모집단으로부터 추출된 표본의 크기 n이 충분히 크면(30 이상), 모집단의 분포 모양과는 상관없이 표본 평균들이 이루는 분포(표본 평균 분포)는 평균이 μ이고, 표준편차가 σ/n제곱근인 정규분포에 근사하게 된다
- 모집단의 크기가 매우 크거나 무한하거나 모집단이 작더라도 복원추출함
- 모집단이 정규분포가 아님
- 표본분포의 정규분포로의 확률적 수렴을 나타내는 정리
- 여기서 n은 표본 평균들의 개수가 아니라 추출할 표본의 크기를 의미
- 모집단이 정규분포가 아니더라도 표본의 크기가 충분하고 데이터가 정규성을 크게 이탈하지 않는 경우 여러 표본에서 추출한 평균은 종모양의 정규곡선을 따름
- 모집단의 분포모양과는 상관없이 표본의 크기가 커지면 표집분포가 정규분포를 이루어 정규분포의 성질을 쉽게 이용할 수 있음
중심극한정리는 표분의 크기가 충분히 클 때 표본 평균의 분포가 모집단의 분포와 관계없이 정규분포로 수렴한다는 수학적 근거를 제공해, 통계량을 이용해 모수를 추정(수학적 확률 판단)할 수 있도록 도와줍니다.
모집단의 크기가 작을 때
모집단의 크기가 작은 유한모집단이거나 비복원추출일 때는 표본평균의 표준편차를 다음과 같이 조정합니다.
- 모집단이 작을 때
- : 모집단의 크기
- : 표본의 크기
- : 조정계수(correction factor)
표본 분산의 표집분포
표본 분산 역시 표본 평균과 마찬가지로 확률분포를 가집니다. 그럼 표본분산 은 어떤 분포를 이룰까요? 표본분산 의 분포는 알려지지 않았습니다. 하지만, 에 (n-1)/을 곱해준 값은 자유도가 n-1인 카이제곱분포(chi-square distribution)를 따릅니다. 여기서 n은 샘플(확률변수)의 개수이고 은 모분산입니다.
자유도가 n이 아니라 n-1인 이유는 모평균 이 표본 평균 로 추정되어 알고 있는 값으로 간주되기 때문입니다. 이미 정해져서 자유롭지 않은 값이 있으면 그 값의 개수만큼 자유도는 줄어듭니다. 은 상수이기 때문에 표본분산 의 분포도 카이제곱분포를 따릅니다.
표준정규분포의 제곱의 합으로 만들어진 분포, 표준정규모집단(모집단의 평균이 0, 표준편차가1이 되는 표준정규분포하는 것)에서 얻은 n개의 데이터를 관측하여 각 데이터를 제곱해서 더한 통계량의 분포, n개의 서로 독립적인 표준정규 확률변수를 각각 제곱한 값을 더한 것의 분포, 표본분산(표본통계량)이 이루는 분포
- 표본의 각 관측값(확률변수)은 동일 모집단에서 추출되었으며 서로 독립적임(i.i.d.)
- 확률변수는 표준정규분포를 따름
- 감마분포에서 α=v/2, λ=2 인 분포, 즉 Γ(v/2,2)
- 비대칭 모양이며 오른쪽으로 꼬리가 긴(right skewed) 분포로 항상 양수값을 갖음
- 자유도가 커질수록 카이제곱분포는 정규분포와 가까워짐
- 개수 집합에 대해 카이제곱 값이 낮다는 것은 기대 분포를 거의 따르고 있음을 나타냄
- 카이제곱 값이 높은 것은 기대한 것과 현저하게 다르다는 것을 나타냄
모집단으로부터 크기가 동일하게 선택가능한 모든 표본을 뽑아서 각 표본의 분산을 계산했을 때 표본분산이 이루는 분포, 표본 평균들의 분산이 이루는 분포
- : 모분산
- : 표본분산
- : 자유도
- 표본 분산의 표집/표본분포는 카이제곱분포를 따름
- 모집단 평균은 표본 평균으로 추정되어 이미 알고 있는 값이기 때문에 n에서 1을 빼줌(n-1개는 값을 모르고 변동이 있는 자유롭게 값을 가질 수 있음을 의미)
표본 비율의 표집분포
모집단이 정규분포일 때 한 모집단으로부터 추출된 분포에서 표본비율의 확률분포는 표본평균의 확률분포와 마찬가지로 표준정규분포를 따릅니다.
동일한 모집단에서 선택가능한 모든 표본을 뽑아 구한 비율들의 분포
- 성공횟수의 기댓값과 분산이 다음과 같을 때
지금까지 모수를 구하기 위해 모집단에서 여러 개의 표본을 뽑아 만든 표본평균의 표집분포, 표본분산의 포집분포, 표본비율의 표집분포를 알아보았습니다.
2단계: 추정
현실에서는 위 경우처럼 많은 표본을 수집하는 것이 어렵습니다. 비용에 따른 제약이 있기 때문입니다. 이 경우 하나의 표본으로부터 표본의 성격을 나타내는 통계량을 기초로 하여 모수를 알아내는 추정(estimation) 방법을 사용할 수 있습니다.
정의
추정을 반복하여 얻은 결과들을 기준으로 일정한 패턴을 찾아낸 후, 미래에 활용할 수 있는 특정한 모수를 가늠하는 것
- 일기예보에서 강수 확률에 대한 과거 자료를 기준으로 현재의 날씨를 분석하고, 일정한 패턴을 매년 측정하여 오늘(미래)의 날씨를 예측하는 것
모집단에서 추출한 표본 특성에 기초하여 미지의 모수에 대해 추측/추론을 하는 추론 과정, 관측 데이터(표본)로부터 미지의 어떤 값을 찾는 것
- 모수에 대해 사전지식이 별로 없을 때
- 예측과 다름
표본으로부터 구할 수 있는 통계량 가운데 가장 적절한 통계량을 선택하는데 이때 모수를 추정하기 위해 사용되는 통계량을 추정량(estimator)이라 합니다. 모평균(μ)을 추정하기 위한 표본평균(X̄) @ 모분산(σ²)을 추정하기 위한 표본분산(S²)은 모두 추정량입니다. 한편, 추정량은 추정치(estimate)와 다릅니다. 추정치는 특정 표본으로부터 계산된 추정량의 실제 값입니다.
모집단의 모수를 추정하기 위해 표본 데이터를 사용하여 계산된 통계량, 모수를 추정하기 위한 함수 또는 공식, 추정값 계산을 위한 통계량, 샘플의 함수(a function of the samples)
- 알려지지 않은 파라미터를 추정
- 가지고 있는 데이터(샘플)의 함수 형태로 나타남
- 모집단의 표본에서 나온 표본 통계량(표본 평균, 표본분산 등)은 모두 추정량이 될 수 있음
- 이때 추정량은 어떤 표본분포를 띈 확률변수가 됨
- 즉, 추정량은 관측된 표본에 따라 모수를 추정하는 것으로써 관측 표본 때 마다 그 값이 달라지게되는 확률변수(랜덤변수)임
- 표본 평균 통계량
특정 표본으로부터 계산된 추정량에 실제 표본 데이터를 대입하여 계산된 값
- 100명의 학생 키를 측정하여 계산한 표본 평균 170cm
- 주식 수익률 데이터로 계산한 표본 분산 0.04
기준
그럼 표본으로부터 구할 수 있는 통계량 가운데 가장 적절한 통계량은 어떤 기준으로 결정할까요? 좋은 추정량은 다음 네 가지 조건으로 결정할 수 있습니다.
- 불편성(unbiasedness)
- 효율성(effciency)
- 일치성(consistency)
- 충분성(sufficiency)
첫 번째 조건은 좋은 추정량의란 편의(bias)가 없습니다.
치우침, 부정확성의 양, 표본추출과정 또는 측정 과정에서 발생하는 계통오차
- 표본을 추출할 때 모집단의 구성원 중에서 특수한 성격을 가지고 있는 구성원을 선호하는 경향
- 표본의 크기를 늘린다 해도 편의 때문에 발생하는 표본추출오차는 줄어들지 않음
원래 대표되도록 의도된 모집단으로부터 추출되지 않고 유의미한 비임의 방식으로 표본이 추출된 것
관측 데이터를 선택하는 방식 때문에 생기는 편향, 데이터를 선택적으로 고르는 관행
또한, 좋은 추정량은 추정하고자하는 모수의 실제값(모수 통계량)에 매우 가깝거나, 그 주위에 집중되는 경향을 보입니다. 통계학에서는 좋은 추정량을 선택하기 위해 다음의 4가지 주요 기준을 중요시합니다.
편의(치우침)이 없는 성질
- 어떤 통계량의 기댓값이 모수에 일치하게되는 통계량을 불편추정량(unbiased estimate) 또는 비편향추정량이라고 함
- 표본평균은 모평균의 불편추정량
- 표본분산은 모분산의 불편추정량
- 표본비율은 모비율의 불편 추정량
- 두 표본평균 차이는 두 모평균 차이의 불편 추정량
표본 크기가 커질수록, 추정량이 모수에 점근적(asymptotic)으로 근접하는 성질
- 표본분산(표본표준편차)
여러 불편의 추정량이 있을 경우, 이들 중 추정량 분산이 더 작게 나타나는 성질
어떤 추정량이 모수 θ에 대해 가장 많은 정보를 제공하는가 여부를 나타내는 성질
종류
그러면 표본으로부터 구할 수 있는 통계량 가운데 모수를 추정하기에 가장 적절한 것은 어떻게 선택할까요? 방법은 점추정(point estimation)과 구간추정(interval estimation)에 있습니다. 점추정은 모수를 단일 값으로 추정하는 방법이고 구간 추정은 모수가 포함될 것으로 예상되는 범위를 제시하는 방법입니다.
점추정
하나의 단일 값으로 모수(모집단의 수치적 특성)를 추정하는 것, 알려지지 않은 파라미터의 값을 하나의 값 또는 하나의 점으로 추정
- 추정량이 모수와 얼마나 가까운지 알 수 없음
- 표본크기가 클수록 추정이 정확해지는 효과를 반영 못함
- 표본 평균 167.5cm를 사용하여 모집단의 평균 키를 추정하는 경우
미지의 모수를 가장 잘 추정하는 표본통계량 (표본 평균, 표본분산, 표본비율 등)
- 표본통계량 중 모수를 추정하기에 가장 적절한 것을 골라서 그 값을 모수로 취하려고 함
- 표본 평균(X̄)은 모집단 평균(μ)의 점추정량
추정량으로부터 계산된 실제 값
= point estimated value구간추정
미지의 모수(참값)가 포함될 것으로 기대하는 신뢰구간을 확률적으로 추정하는 통계적 추정 방법, 일정한 확신(신뢰수준)으로 일정한 구간(신뢰구간) 안에 모수가 있을 가능성이 얼마인가를 추정하는 것, 일정 확신으로 모수가 포함될 신뢰구간을 추정하는 것, 추정한 값이 구간, 즉 특정값과 특정값 사이에 있다고 유연하게 추정하는 것
- : 모수
- : 파라미터 θ의 점추정량
- 신뢰 구간을 사용하여 모수의 가능한 범위를 제시
- 점추정량에 대해서 상수값과 표준편차의 곱을 빼고 더한 구간으로 정의됨
- 표본크기에 따라 추정의 정확성에 영향을 받으며 추정 가능
- 구간으로 추정하여 보다 유연한 정보 제공
모수를 추정하기 위해 사용되는 구간을 계산하는 방법이나 공식
실제 표본 데이터를 사용하여 구간추정량을 적용한 결과로 얻어진 구체적인 구간 값
모수가 포함되리라고 기대되는 구간, 모수가 포함될 것으로 추정된 구간
- : θ의 점추정량
- 구간 범위로 추정값을 표시하는 방법
- 참값이 일정 구간안에 있을 확률에 대한 대답을 설명하는 근거
- 표본추정치 주위의 x% 신뢰구간이란 비슷한 샘플링 절차를 따랐을 때 평균적으로 유사한 표본추정치 x% 정도를 포함
- 구간이 넓어진다는 의미는 불확실성이 더 커진다는 뜻
- 신뢰수준이 높을수록, 표본이 작을수록 구간이 넓어짐
- 더 많은 데이터를 보유할수록 표본추정치의 변이가 줄어듬
- 95% 신뢰구간? 표본통계량의 부스트랩 표본분포의 95%를 포함하는 구간
신뢰구간의 최상위, 최하위 끝점
신뢰구간의 최하위 끝점
신뢰구간의 최상위 끝점
신뢰한계 안에 모수가 포함될 확률, 같은 모집단으로부터 같은 방식으로 얻은, 관심 통계량을 포함할 것으로 예상되는 신뢰구간의 백분율
- 허용할 수 있는 신뢰수준이 낮을수록 신뢰구간은 좁아짐
모평균
모평균의 신뢰구간을 추정할 때는 모표준편차를 아는 경우와 알지 못하는 경우로 나뉩니다. 모표준편차를 알고 모집단이 정규분포를 이룬다면 표준정규분포(Z 분포)를 사용하여 신뢰구간(모수를 포함할 것으로 추정된 구간)을 추정할 수 있습니다. Z 점수를 구하는 공식은 다음과 같습니다.
$$Z=(\overline{X} - \mu_{\overline{X}})/\sigma_{\overline{X}}$$
여기서 $$\mu_{\overline{X}}$$은 표본평균의 평균이며 $$\sigma_{\overline{X}}$$은 표본평균의 표준편차입니다.
- : 표본 평균, \sigma_{\overline{X}}
모표준편차를 알지만 모집단은 정규분포가 아닐 경우에도 표본의 크기가 충분히 크다면(30 이상), 중심극한정리에 의해 위 식을 적용하여 모평균의 신뢰구간을 추정할 수 있습니다.
하지만, 모표준편차는 일반적으로 알려져 있지 않습니다. 모집단의 표준편차는 모집단의 대개 모집단의 평균을 알아야 구할 수 있기 때문입니다. 즉, 현실 상황에서는 위 방법을 사용하여 모평균의 신뢰구간을 추정할 수 없습니다. 따라서 모표준편차를 모르는 경우에는 표본에서 구한 불편추정량 , 즉 표본의 표준편차를 모집단의 표준편차 대신 사용합니다. 이때 표본의 크기에 따라 두 가지 방법으로 나뉩니다.
표본의 크기가 큰 경우(일반적으로 n ≥ 30)에는, 중심극한정리에 따라 근사적 Z-분포를 사용할 수 있습니다. 표본의 표준편차와 모집단의 표준편차의 차이가 작기 때문입니다. 이 경우 모평균의 신뢰구간을 구하는 공식은 다음과 같습니다:
$$\overline{X} \pm Z_{\alpha/2} \cdot \frac{S}{\sqrt{n}}$$
반면, 모표준편차를 모르며 표본의 크기가 작을 때는 Z점수를 구하는 공식에서 분모에 $$\sigma_{\overline{X}} = \frac{\sigma}{\sqrt{n}}$$ 대신 $$S_{\overline{X}} = \frac{S}{\sqrt{n}}$$를 사용합니다. 이 때 $$(\overline{X} - \mu_{\overline{X}})/S_{\overline{X}}$$는 표준정규분포를 따르지 않고 자유도 n-1인 t-분포를 이룹니다. 따라서, 우리는 t-분포를 이용해 신뢰구간을 구해야 합니다. t-분포는 주로 모집단의 표준편차가 알려져 있지 않고 소표본에서 정규분포 대신에 모평균을 추정할 때 사용합니다.
- : 자유도
- 표준정규분포와 카이제곱분포의 결합으로 이루어진 분포로 대표적인 비정규분포
- 0을 중심으로 좌우대칭이며 가운데 종모양 부분은 Z분포보다 낮고 꼬리 부분은 약간 더 두껍고 김(표준정규분포보다 t 분포의 분산이 더 크기 때문)
- 표본이 클수록 표준정규분포와 닮은 t분포가 형성됨(자유도 30 이상)
- 모집단 표준편차를 모를 때 표본 평균과 모집단 평균 사이 표준화된 거리, 표본통계량의 분포(표본 평균, 두 표본 평균 간의 차이, 회귀 파라미터 등)를 설명하는 데 광범위하게 사용됨
모집단의 분포가 평균이 이고 분산이 인 정규분포를 이루고 해당 모집단에서 독립적으로 n개의 표본을 뽑았을 때, 정규분포로부터 t-분포는 다음과 같이 추정할 수 있습니다.
표본통계량이 표본평균일 때 이를 표준화(정규화)시킨 표본 분포
- 모집단이 정규분포를 이룸
- 표본의 각 관측값(확률변수)은 동일 모집단에서 추출되었으며 서로 독립적임(i.i.d.)
- 모집단의 분산을 모르거나 표본 크기가 작음(n < 30)
- : 표본크기
- : 표본 평균
- : 모평균
- : 표본표준편차
- 표준정규분포와 t 분포의 차이는 분모에 모표준편차를 사용했는지 표본 표준편차를 사용했는지로 나뉨
- 표본평균의 분포는 일반적으로 t 분포와 같은 모양
- : 표본 평균
방법
추정량을 도출하기 위해서는 다양한 통계적 방법, 즉 추정법(method of estimation)을 사용합니다. 추정법은 미지의 모수에 대해 최적의 방법을 찾아가는 체계적 방법론이라고 해서 알고리즘(algoritm)이라고도 합니다.
잔차 제곱의 합을 최소화시키는 추정 방법
- 다중회귀모델에서 사용
- 확률분포를 고려치 않고도 추정량을 구하는 법
- 평균과 마찬가지로 특잇값에 매우 민감하다는 단점이 있음
- 선형회귀모델의 파라미터를 추정하는데 사용됨
평균제곱오차(MSE)가 최소가 되도록 추정량을 만드는 것
특정 확률분포를 가정하여, 그때 최대우도를 보이는 추정량을 구하는 법
- 관측값을 보고 여러 가설들을 평가할 때의 측도
- 로지스틱 회귀모델의 파라미터를 추정하는데 사용됨
- 점추정량을 구하는 가장 오래된 방법
- 모집단 확률분포를 알지 못해도, 모집단 적률에 대한 추정량을 구할 수 있는 방법
사후확률을 최대화시키는 부류로 추정 분류하는 결정규칙
평가
통계적 추정(estimation)의 정확성(accuracy)에 대한 질적인 척도, 추정값이 참값에 과연 어느정도 근접하는가를 척도화(정량화)한 것
측정값에서 오차의 크기
- 절대오차가 0에 가까울수록 정확도가 높아짐
- 상대오차가 0에 가까울수록 정확도가 높아짐
모든 절대오차의 평균
- 이상치가 많을 때
- : 샘플수
- : 관측값
- : 추정값
잔차의 제곱에 대해 평균을 취한 값, 오차의 제곱에 대해 평균을 취한 것
- 최소평균제곱오차법(MMSE) 등에 쓰임
- : 기댓값
- : 확률변수
- : 추정량
잔차의 제곱에 대해 평균을 취하고 이를 제곱근한 값, 오차의 제곱에 대해 평균을 취하고 이를 제곱근한 것
- 회귀모형을 평가(회귀분석, 최소제곱법 등에)하는 데 가장 널리 사용되는 측정 지표
- 회귀 시 평균제곱오차의 제곱근
MSE, RMSE 등이 작을수록 추정의 정확성이 높아집니다.
잔차의 표준편차, 평균제곱오차와 동일하지만 자유도에 따라 보정된 값, 표본 집단에 기초해 산출된 기대값(추정값)과 확률시행 결과의 관측값의 차이, 회귀직선(추정곡선) 등을 통해 얻은 추정값과 실제 관측치와의 차이
= 추정오차(estimation error)나타난 결과에 따라 여러 가능한 가설들을 평가할 수 있는 측도(measure)
= 가능성, 가능도나타난 결과에 해당하는 각 가설 마다 계산된 우도 값 중 가장 큰 값
목표는 가지고 있는 데이터를 이용해서 실제 데이터의 값과 최대한 같은 값이 나오도록 하는 파라미터를 찾는 것입니다. 즉, 실제값과 예측값의 차이인 비용함수(cost function)를 최소화하는 파라미터를 찾는 것입니다. 비용함수를 최소화하면 최적의 추정치를 찾을 수 있습니다.
실제값과 모델이 예측하는 값의 차이를 계산하는 함수
- 입력 데이터값들 하나하나에서 실제값과 예측값 간의 오차를 계산하는 방식
- 손실 함수를 Σ으로 나타낸다면 비용 함수임
- 개별적인 오차를 정의
실제값과 모델이 예측하는 값의 차이, 즉 오차를 더하거나 제곱을 취해 모두 합하거나 평균의 형식으로 표현한 함수, 추정치를 얻는 방법의 성능 척도 또는 추정의 정확성을 정량화하기 위한 척도를 일반화한 함수
- : f(X)의 추정하기 이전 파라미터
- : f(X)의 추정한 이후 최적 파라미터
- 손실함수를 모두 더해서 평균을 취한 형태
- 모델 f(X)의 종류는 여러 가지가 있음
- 실제값과 모델로부터 나온 값의 차이의 제곱의 합을 최소로 하는 파라미터를 찾는 것이 중요
- 최적화 문제에서는 비용함수를 목적함수(objective function)라고 함
3단계: 가설검정
정의
귀무가설과 대립가설을 설정하고 추출한 표본을 이용하여 얻은 어떤 관찰값(검정통계량)을 기반으로 두 가설 중 어떤 가설을 기각하고 채택할지를 결정하는 것, 알려지지 않은 파라미터에 대한 가설을 세우고 그 가설이 옳은지의 여부를 확률적으로 판단하는 것, 모수에 대해 약간의 지식이 있을 때 가설의 타당성을 판단해보는 통계적 추론, 모집단에 대한 가설을 해 보고 이의 진위를 검정통계량에 기초하여 검정을 하는 것, 표본을 이용하여 미지의 모집단 모수에 대한 두 가지 가설을 놓고 어느 가설을 선택할 것인지 통계적으로 의사결정을 하는 것, 표본 자료를 이용해 모집단 값에 대한 주장을 평가하는 과정, 표본의 성격을 나타내는 통계량을 기초로 하여 모수를 추정하는 통계적 분석방법, 관측된 데이터(실험 결과 일어난 확률)로부터 모집단에 대한 가설을 설정하고 표본을 통해 얻는 정보에 따라 그 타당성을 검증하는 방법, 주장하고 싶은 것과 반대되는 가설을 설정하고 설정한 주장이 성립하기 어려운 점을 보여 반증하는 방법
- 무작위 추출: 표본을 모집단으로부터 추출할 때 무작위로 추출해야 함
- 통계적 독립성: 표본으로부터 관측치를 수집할 때 어떤 하나의 관측치가 다른 관측치에 영향을 미치지 않아야 함
- 정규성: 표본을 구성하는 관측치는 충분히 많아서 분포가 정규분포를 구성해야 함
- 등분산성: 둘 이상의 표본을 비교하는 가설검정을 하는 경우 이 두 집단은 서로 등분산을 구성
- 표본의 크기: 표본의 크기를 늘리면 표준오차가 줄어들어 모수에 접근하게 되므로 통계적 검정력은 높아짐
- 1) 가설 설정: 기각하고 싶은 귀무가설과 채택하고 싶은 대립가설을 설정한다
- 2) 확률분포와 유의수준 설정: ① 어떤 확률분포로 검정할 것인지 ② 어느 정도의 확률로 귀무가설을 기각할 것인지 그 판정 기준(유의수준)을 정한다
- 3) 유의수준을 충족시키는 임곗값 설정
- 4) 검정 통계량과 확률 계산: 귀무가설하에서 검정통계량(표본평균, 표본비율, 표본분산 등)과 검정통계량이 관측되는 확률을 계산한다
- 5) 통계량과 임곗값 비교 및 가설 판정: 확률이 기준보다 클 경우 귀무가설을 수용(귀무가설이 옳을지도 모른다, 흔히 있는 일이 일어났을 뿐), 확률이 기준보다 작을 경우 귀무가설을 기각(귀무가설은 옳지 않다, 좀처럼 일어나지 않는 일이 일어났다!, 대립가설 쪽이 옳을 듯 하다)
귀무가설이 옳은지 아닌지를 판단하는 것
용어
주어진 사실 혹은 조사하고자 하는 사실이 어떠하다는 주장이나 추측, 미리 모집단에 대해 세워둔 주장, 어떤 모집단의 모수에 대한 잠정적인 주장
- 귀무가설과 대립가설로 나뉨
표본 사이에 통계적으로 의미가 없다고 예상되는 가설, 일반적으로 믿어온 사실을 가설로 설정한 것, 연구에서 주장/채택하고 싶은 내용과는 반대되는 가설, 연구에서 주장하고 싶지 않은(기각하고 싶은) 가설, 연구과정에서 직접 검정의 대상이 되는 가설, 모집단의 모수에 대한 가설
- 현실적으로 검정할 수 있는 가설을 귀무가설로 설정
- 흔한 가설, 기존의 알려져 있는 사실, 현재의 사실
- 검정은 이 가설을 반증해 보는 것
- 두 집단의 모평균/모분산에 차이가 없다
- ~은 차이/효과가 없다, ~의 평균은 __이다, ~는 집단 간 평균이 같다
- 스포츠 이온 음료의 용량은 제품에 표기된 250ml다
표본 사이에 통계적인 차이가 있다는 가설, 공공연하게 사실로 받아들여진 현상에 대립되는 가설, 검정의 대상이 되는 가설이 받아들여질 수 없을 때 대신 받아들여지는 가설, 귀무가설이 틀렸다고 판단될 때 대안적으로 채택하는 가설, 연구에서 주장하고 싶은 가설
- 흔하지 않은 가설, 새로운 사실, 현재의 믿음에 변화가 있는 사실, 변화된 사실로 연구의 목적이며 대립가설이 지지를 받으면 큰 의미가 생김
- 본래 연구에서 주장하고 싶은 내용
- 실험계획에서 독립변수가 종속변수에 영향을 주는 상황을 가정
- ~평균은 __가 아니다, ~은 효과가 있다, ~는 집단 간 의 차이가 있다
- 양측검정: 스포츠 이온 음료의 용량은 제품에 표기된 250ml가 아니다
- 단측검정: 스포츠 이온 음료의 용량은 제품에 표기된 250ml보다 적다 또는 스포츠 이온음료의 용량은 제품에 표기된 250ml보다 많다
귀무가설을 기각하는 기준이 되는 임계값
- 유의수준 5%: 독립변수가 실제로 종속변수에 효과가 없든데 효과가 있다고 잘못 결론 낼 확률이 5% 미만, 5%의 확률로 1종 오류가 발생할 수 있음
- 유의수준은 전적으로 연구자(조사자)가 결정
- 통계적 가설 검정 시 1종 오류를 1% 또는 5% 이내로 설정함
주어진 유의수준에서 귀무가설의 채택과 기각에 관련된 의사결정을 할 때 기준이 되는 경계값
- 검정통계량을 계산하여 임계치를 기준으로 좌/우 어느 쪽에 있는가에 따라 채택과 기각을 판단함
통계적 가설을 검정할 목적으로 귀무가설이 참이라는 가정 아래 얻은 표본통계량, 표본통계량을 계산했을 때 귀무가설이 가지는 값이 모수로부터 어느 정도 떨어져 있는지를 나타내는 지표, 추출한 표본(데이터)을 이용하여 얻은 어떤 관찰값
- 검정통계량이 크면 어떤 데이터로부터 나온 값과 귀무가설에서 주장하는 바의 차이가 크다 -> 귀무가설이 틀릴 확률이 높아짐 -> 귀무가설 기각
- 검정통계량이 작으면 표본에서 얻은 값과 귀무가설에서 주장하는 바가 차이가 크게 없음을 의미 -> 귀무가설 채택
귀무가설에서 주장한 바가 옳을 확률, 검정통계량이 얼마나 큰지를 통계적으로 판단하기 위해 0과 1사이의 확률값으로 보여주는 지표, 귀무가설이 참이라는 가정 아래 얻은 검정통계량이 귀무가설을 얼마나 지지하는지를 나타내는 확률, 귀무가설이 참일 때 표본 분포에 추출한 표본 검정 통계량이 나올 확률
- : 검정통계량
- 귀무가설을 채택할지 기각할지의 기준으로 사용할 수 있는 값
- 검정통계량과 p-value는 반비례
- p-value < 유의수준 0.05(0.01): 검정통계량이 매우 큼, 표본통계량이 우연히 나타나기 어려운 케이스(예: 표본 평균이 표본평균분포 하에서 관측될 확률이 낮음)를 의미하기 때문에 귀무가설을 기각하고 대립가설을 채택
- p-value > 유의수준 0.1: 검정통계량이 작음, 귀무가설이 참일 확률이 매우 큼
- p값은 다른 수치를 표준화한 효과를 가지고 있어 거의 모든 분석 결과에서 사용함
효과가 없는 상황인데 있다고 판단해서 발생하는 오류, 귀무가설이 참인데 기각함으로써 발생하는 오류, 독립변수에 따른 효과가 없는데 있다고 잘못 판단하는 오류
- 가설검정에서는 1종 오류만 고려
- 단, 무작정 1종 오류를 줄릴 수는 없기 때문에 1종 오류가 나타날 가능성의 임계값을 1% 또는 5%로 설정하고 귀무가설을 판단
- α는 유의수준(significance level)이라고 함
- 유의수준 5%란 효과가 없는데 있다고 잘못 결론 낼 확률이 5% 미만이며, 표본을 추출해서 나온 검정 통계량(차이, 효과)이 우연히 나타날 확률은 5% 미만임을 의미
- 실제로 신약이 효과가 없는데 있다고 판단
귀무가설이 거짓이어서 귀무가설을 기각해야하는 데 채택함으로써 발생하는 오류
- 2종 오류는 가설 검정의 검정력(statistical power)와 관련 있음
- 실제로 신약이 효과가 있는데 없다고 판단
종류
모수/비모수
정규성 가정이 필요한 검정
- t-검정
- 분산분석(ANOVA)
정규성 가정이 필요 없는 검정
표본 수
한 집단의 평균을 특정 값과 비교, 관측된 한 개의 표본통계량을 이미 알고 있는 특정 통계량(평균, 분산 비율 등)과 비교한 다음, 이들이 모집단에서도 다른지 어떤지 확률적으로 판정하는 방법
- 특정 값(모평균)과 표본평균 검정
- 특정 값(모비율)과 표본비율 검정
- 특정 값(모분산)과 표본분산 검정
조건이나 처리에 따라 두 그룹으로 나누었을 때, 관측된 두 표본통계량(평균, 분산, 비율 등)이 모집단에서도 다를지 아닐지 확률적으로 판단하는 방법
- 독립표본 검정: 독립된 두 집단의 평균 비교
- 대응표본 검정: 동일 집단의 전후 비교
- 일원배치 분산분석: 3개 이상 집단의 평균 비교
- 다중비교: 본페로니 교정 등의 방법 사용
용어
두 모집단으로부터 표본을 각각 추출할 때 표본을 구성하는 각각의 인자가 짝을 지어 서로 연관된 표본
- 교육, 광고, 의료 등의 분야에서 사전(ex-ante)과 사후(ex-post)를 비교하여 효과를 평가할 때 주로 사용
두 모집단으로부터 각각 표본을 추출할 때 각 표본을 구성하는 인자가 서로 상관없는 표본
데이터 유형
- t-검정: 모집단의 평균을 검정
- 분산분석(ANOVA): 3개 이상 집단의 평균 차이 검정
- 카이제곱 검정: 범주형 변수 간의 관련성 검정
가설 방향
가설검정에서 기각영역이 어느 한쪽에만 있는 검정
- 우측검정: 증가 방향만 검정
- 좌측검정: 감소 방향만 검정
가설검정에서 기각영역이 양쪽에 있는 검정
용어
방법
Z-검정
표본평균을 표준화한 z분포를 사용하는 검정 방법
- 1개 모집단 검정
- 모분산을 아는 경우
- 모분산을 모르지만 표본이 아주 큰 경우
- : 검정통계량 z값(z-value)
- : 모표준편차
- : 표본표준편차
- 표본의 크기가 크면 편의상 Z-분포를 사용함: 모집단의 정규성과 상관없이 중심극한정리에 의해서 표집분포는 정규분포가 되어 t와 Z 두 분포의 차이가 없어짐
t-검정
표본평균을 스튜던트화한 t 분포를 사용하는 검정 방법
- 표본의 크기가 충분하지 못한 경우
- : 검정통계량 t값(t-value)
- t검정이 z검정보다 큰 개념
- 분자의 표본의 표준편차는 패널티 역할을 하고(표준화를 해서 분산이 결과에 영향을 주는 것을 상쇄), 분모의 데이터의 개수는 보상의 역할을 함
- 1개 표본에 대한 t 검정(one sample t test)과 2개 표본 평균 차이에 대한 검정(two sample t test)로 나뉨
카이제곱검정
- 1개 모집단의 분산 검정
F-검정
세 그룹 이상의 분산이 같은지 아닌지를 판정하는 검정 방식, 두 정규분포의 분산 모수가 같은지를 확인하는 검정 방식
- 2개 모집단 간 분산 비교 검정
- 바틀렛(bartlett), 플리그너(fligner), 레빈(levene) 검정을 주로 사용
- 공장 A의 나사 차이 vs 공장 B의 나사 차이: 공장 A에서 제조된 나사와 공장 B에서 제조된 나사의 길이는 차이가 있을까?
카이제곱분포의 비율로 정의되는 분포
- : 자유도
- 2개 이상의 표본평균들이 동일한 모평균을 가진 집단에서 추출되었는지 아니면 서로 다른 모집단에서 추출된 것인지를 판단하기 위해 사용
F 통계량을 확률변수로 취하는 표본분포, 표본통계량이 두 독립 표본에서 계산된 표본분산들의 비율일 때의 표본 분포, 분산의 비에 관한 분포
- 자유도가 1인 경우에는 지수분포와 같은 모양을 가짐
- 자유도가 2부터는 오른쪽으로 긴 꼬리를 가진 카이제곱분포와 비슷한 모양을 가짐
- 2개 이상의 표본평균들이 동일한 모평균을 가진 집단에서 추출되었는지 아니면 서로 다른 모집단에서 추출된 것인지를 판단하기 위해 사용
목표
모평균
관측된 표본평균을 특정 값(이미 알고 있는 모평균)과 비교하고 두 값이 같을지 다를지를 확률로 판정하는 방법, 관측된 표본평균을 특정 평균과 비교하는 검정 방식
- 가장 기본적인 가설검정
- 회귀계수의 t검정에 이용
- 카탈로그 연비 vs 사용자가 계측한 실제 연비: 카탈로그에 게재되어 있는 A차종의 연비와 사용자가 계측한 실제 연비에 차이가 있을까?
- 과자 용량 표기 무게 vs 실제 과자 용량: 어느 과자제품의 겉봉지에 용량이 200g이라 표시되어 있다. 과연 표시된 용량만큼 과자가 들어있을까?
- 기존 방식으로 만든 전구 수명 vs 새로 개발한 전구 수명: 어느 전구공장에서 새로 개발한 전구가 과거의 것보다 훨씬 전구의 수명이 길다고 선전한다. 과연 이 선전이 믿을만한가?
모집단 2개
모집단이 2개일 때는 두 개의 모집단의 평균이 서로 차이가 있는지를 파악하는 것이 목표입니다. 모집단의 평균 차이는 각 모집단에서 추출한 표본 집단의 평균 차이를 이용해 구할 수 있습니다.
- 수립된 가설에 대한 검정은 자유도를 (n-1)로 하는 t분포 이용
두 그룹(집단, 조건, 처리)의 평균을 비교해서 이들의 차이가 모집단에도 있다고 해도 좋을지의 여부를 확률로 판정하는 검정 방식
- 합동분산추정량은 서로 독립적인 모집단들의 공통 분산의 불편추정량
- 대응이 없는 데이터(unpaired data): 다른 개체를 같은 조건으로 측정한 데이터 ex) 성별 검사
- 대응이 있는 데이터(paried data): 같은 개체를 다른 조건으로 측정한 데이터 ex) 약의 사용 전후, 강습회 수강 전후
- 한 반의 남자 성적의 평균 vs 한 반의 여자 성적의 평균: 남자 집단의 성적과 여자 집단의 성적에 차이가 있을까?
모집단 3개
3개 이상의 모집단의 평균이 같은지를 알고 싶을 때는 분산분석을 이용합니다. 분산분석은 집단의 분산을 이용하여 모평균을 비교 분석한다는 점에서 t-검정과 다릅니다.
3개 이상의 모집단을 검정하는 방법론
- 3개 모집단 간 평균 비교 검정
- 독립변수: 요인(factor), 모집단/범주: 수준(level), treatments
하나의 독립변수를 여러 개의 수준으로 나누어 각 수준의 효과에 차이가 있는지를 알아보는 가설검정 방법, 3개 이상의 모집단의 평균 차이를 비교 검정하는 방법
- : 수준 i에서 j번째 관측치
- : 수준 i의 관측치들의 평균
- : 독립적인 확률오차
- : 수준 i의 관측치들의 평균에 대한 점추정량
- : i번째 수준의 평균(Y i dot bar)
- : 전체 평균에 대한 점추정량
- : 전체 평균(Y dot dot bar)
- : 관측치 개수
- : 수준의 개수
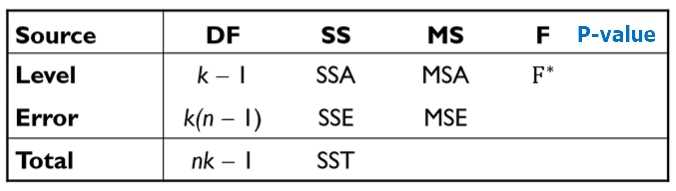
- 분산분석은 항상 양측 검정임
- 분산분석은 적어도 2개 평균이 다르다는 것을 찾아주지만, 구체적으로 어떤 평균이 다른지는 알 수 없음, 어떤 평균 사이에 차이가 있는지를 알고 싶다면 다중비교분석(multiple comparison test)를 할 수 있음
- SST, SSA, SSE는 모두 분산이므로 카이제곱분포를 따름, 두 카이제곱분포를 자기 자신의 자유도로 나눈 분포는 F 분포를 따르므로 F 검정을 이용할 수 있음
- F 검정통계량이 큰 값을 갖는다는 의미는 집단 간 변동성이 집단 내 변동성보다 크다는 뜻
- SSA > SSE 이면, 즉 레벨 간 차이가 레벨 내 차이보다 크다면 수준 간 차이가 있음, SSA/SSE이 큰 값 이면 귀무가설을 기각
- SSA < SSE 또는 SSA/SSE <1 이면, 즉 레벨 간 차이가 레벨 내 차이보다 작다면 원래 변동이 심한 것, SSA/SSE이 작은 값이면 귀무가설을 채택
모분산
평균에 대해 어느 정도의 산포가 나타나는지를 살펴보는 가설검정, 관측된 표본분산을 특정 분산 값과 비교하고 그것이 다른지 아닌지를 카이제곱분포를 사용해 판정하는 검정 방식
- 안정성을 중시하는 품질관리 등에 이용
- 허용할 수 있는 내용량 차이 vs 어느 제조 라인의 내용량 차이: 어느 생산 라인에서 제조된 과자 한 봉지의 용량이 허용 기준에 못 미칠까?
- 회사 A가 생산하는 볼트 직경의 분산 vs 회사 B가 생산하는 볼트 직경의 분산
모비율
관측된 표본비율을 특정 비율 값(이미 알고 있는 특정 모비율)과 비교하고 그것이 다른지 아닌지를 정규분포를 사용해 판정하는 검정 방식
- 찬성률, 질병률, 원료에 대한 제품 비율 등에 이용
- 목표 지지율 vs 설문조사에서 나타난 지지율: 지지율이 30% 이하로 내려가면 내각을 해산하고 싶은데, 설문조사에서는 지지율이 20%였다. 과연 해산해야 할까?
- 금년도 대통령 선거에서 특정 후보의 지지율이 과연 50%를 넘을까?
- 작년도 실업률이 7% 였는데 올해의 실업률은 높아졌는가?
- 100명의 고객이 AS 서비스를 받았을 때 몇 %의 고객이 만족감을 느꼈을까?
두 조건(그룹, 집단) 하에서 모비율에 차이가 있는지 없는지를 판정하는 검정 방식
- : A반 표본의 크기
- : B반 표본의 크기
- A라인의 수율 vs B라인의 수율: A라인에서 제조된 액정 패널과 B라인에서 제조된 액정 패널은 수율의 차이가 있을까?
- A대학교의 A반은 스마트폰 어플리케이션을 이용해서 출석 확인을 하고 B반은 기존의 호명으로 출석을 확인하고 있을 때, A와 B반의 출석률에 차이가 있는지를 검정
통계적 분석
통계적 방법론을 바탕으로 하는 분석
- 비교: X에 따라 Y에 차이가 있는가? - X: 범주형 자료, Y: 범주형 자료/수치자료
- 관계: X와 Y가 관련이 있는가? X가 Y에 영향을 주는가? - X: 수치자료, Y: 수치자료
- 분류: X에 따라 Y를 분류할 수 있는가? X, Y가 비슷한 것끼리 묶을 수 있는가? - X: 수치자료, Y: 범주형 자료
용어
선행하는 어떤 변인이 후행하는 다른 변인의 필연적인 원인이 되는 관계
= 인과관계는 상관관계를 포함함2개 이상의 변수의 선형 관계가 있는 범위를 표현하는 통계적 측도
- 선형 관계에 있는 변수는 상수 비율에 따라 함께 변경됨
X변수만으로 Y를 100% 표현할 수 있는 관계
- 오차항 없음
- 힘 = f(질량, 가속도)
- 주행거리 = f(속도, 시간)
X변수만으로 Y를 100% 표현할 수 없는 관계
- 오차항 있음
- 반도체 수율 = f(설비 파라미터들의 상태, 온도, 습도) + ε
- 포도주 가격 = f(강우량, 온도, 포도품종) + ε
- 위조카드 여부 = f(사용시간, 사용액, 사용장소) + ε
종류
기준1: 독립변수의 수
독립변수(X)가 1개
2개 이상인 독립변수(X)를 함께 관련지어 분석하는 통계적 분석 방법
- 다중 회귀분석
기준2: 종속변수의 수
종속변수(Y)가 1개인 단일 변량에 대한 분석
종속변수(Y)가 2개인 분석
2개 이상의 종속변수(Y)를 함께 관련지어 분석
방법
다변량 수치형 자료는 기본적으로 산점도를 이용해 파악합니다. 산점도를 이용하면 두 수치변수간의 관계를 시각적으로 빠르게 파악할 수 있습니다. 여기서 나아가 두 수치변수 간에 직선관계가 어느 정도인지를 나타내는 통계값이 있습니다. 이 통계값이 공분산(covariance)와 상관계수(correlation coefficient)입니다.
두 확률변수의 분포가 결합확률분포를 이룰 때 해당 분포의 분산, 두 변량(확률변수) 간에 상관성/의존성/유사성의 방향을 나타내는 척도, 두 변량이 각각의 평균으로부터 변화하는 방향 및 크기를 결합시킨 기대값
- 두 확률변수 간에 직선관계가 어느 정도인지 알고 싶을 때
- x와 y의 평균값에서 멀어질 수록 큰 값을 가짐
- x와 y의 평균값을 중심으로 1과 3사분면에 자료가 많고 길게 분포 = 두 변수가 같은 방향으로 변화 = 공분산은 양수(+)
- x와 y의 평균값을 중심으로 2과 4사분면에 자료가 많고 길게 분포 = 두 변수가 변화하는 방향이 서로 다름 = 공분산은 음수(-)
- 직선 관계가 없으면 공분산은 0
- 공분산은 측정 단위에 영향을 받기 때문에 그 값 자체로 선형관계의 정도를 알 수는 없음
- 공분산을 표준화한 것이 피어슨의 상관계수
- 공분산의 단위를 스케일링(scaling)한 것
- 기울기를 가지는 직선에 조밀하게 모일수록 |r|은 1에 근접
예측하고 싶은 결과가 수치일 때 사용하는 통계적 방법
= 수치예측예측하고 싶은 결과가 범주일 때 사용하는 통계적 방법
- 표본으로부터 관측값이 모집단 내 정해진 어떤 부류에 속하는지를 판단
- 제품 불량 여부, 고객 이탈 여부, 보험 사기 여부, 이메일 스팸 여부
상관분석
두 변수가 연속형 변수일 때 변량들 간에 선형적 관계(의존 유무, 두 변수 간의 관계의 강도), 즉 두 변수가 서로 얼마나 밀접하게 관련되어 있는지를 상관계수(correlation coefficient)를 이용해 분석하는 방법
회귀분석
1개의 종속변수와 1개 또는 2개 이상의 독립변수들 간의 관련성을 규명할 수 있는 수학적 모형을 측정된 변수들의 자료로부터 선형 회귀식을 도출하여 모형을 세우고 이를 통해 예측, 분석하는 방법
용어
변수들간의 확률적 관계식을 선형식으로 표현할 때, 기울기를 나타내는 선
회귀선의 기울기, 반응변수에 미치는 예측변수의 가중치(예측변수가 한 단위만큼 변화함에 따라, 반응변수에 미치는 영향력의 크기)
= 기울기, 모수 추정값, 가중치회귀직선의 절편, 즉 X=0일 때 예측값
= 절편예측값을 추정하는 데 생기는 오차
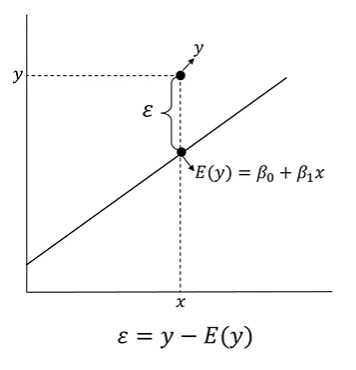
- X로 설명할 수 없는 부분
- 직선식이 확정되기 이전(추정하기 이전)
- 불확실성을 가지고 있기 때문에 확률분포를 따름
모집단에서 추출한 표본들의 평균(표본평균)과 개별 표본값 간의 편차, 데이터 포인트와 예측값 혹은 평균 사이의 차이, 설명 안된 편차(unexplained deviation), 실제 y값과 최소제곱법으로 구해진 직선 위에 있는 점의 차이
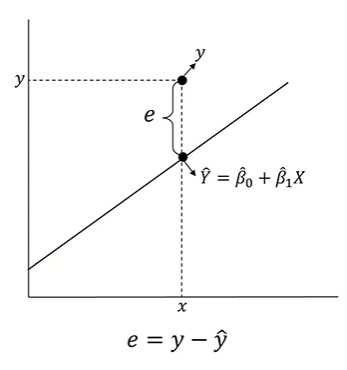
- 확률오차가 실제로 구현된 값
- 직선식이 확정된 이후(추정한 이후)
- 회귀식으로 설명이 안되는 부분
표본회귀식에서 얻은 예측값과 실제 관찰값 사이에서 나타나는 잔차들의 표준편차
- 표본들의 실제 관찰값이 회귀식으로부터 얼마나 흩어져 있는지를 나타냄
- 측정 단위에 영향을 받아 적합도 검정에서는 결정계수(coefficient of determination)를 사용
모델
출력변수 Y를 입력변수 X들의 선형결합으로 표현한 모델
- X변수와 Y변수 사이의 관계를 함수식으로 설명
- 미래의 반응변수 Y값을 예측
- 입력변수(X)와 출력변수(Y) 평균과의 관계를 설명하는 선형회귀식을 찾는 것
- : 변수
- : 확률오차
- Y는 확률변수여서 특정하게 정해진 값이 아님
1개의 입력변수(X)와 출력변수(Y) 평균과의 관계를 설명하는 선형식
비선형회귀분석
응답변수와 예측변수 간의 관계가 반드시 선형일 필요는 없습니다. 비선형회귀(nonlinear regression)는 최소제곱 방법으로 피팅할 수 없는 모델을 의미합니다. 비선형이라는 의미는 예측변수들의 선형결합 또는 일부 변환으로 응답변수를 표현할 수 없는 모든 모델을 말합니다. 약물 복용량에 따른 반응은 일반적으로 비선형성을 띕니다. 복용량을 두 배 늘린다고 두 배의 반응이 나타나지는 않습니다.
회귀모형에 다항식(제곱, 세제곱 등) 항을 추가한 방식
다항 구간들을 부드러운 곡선 형태로 피팅한 것
스플라인 구간을 구분하는 값들
자동으로 구간을 결정하는 스플라인 모델
역설
제3의 요인으로 전체자료를 세분화했을 때 정반대의 결과가 나오는 것
- 가중평균을 이용해 교락 변수 통제
각 집단에서 불행한 사건을 겪으리라고 예상되는 비율
위험요인이 있는 집단의 절대위험도 / 대조군의 절대위험도
- 개개인에 대한 비교를 하는 경우 유용함
- 상대위험도 값이 높아도 절대위험도가 작을 경우 실제적으로 위험하지 않을 수 있음
주어진 집단에서 특정 사건에 일어나는 개수의 예측값
참고 문헌
전체
- [1] 김대학, 「제 2장 데이터의 이해」, 대구가톨릭대학교, "http://contents.kocw.or.kr/KOCW/document/2014/cu/kimdaehak/2.pdf"
- [2] 김성범(소장/인공지능공학연구소), #핵심 확률/통계 Playlist [비디오 파일]. 검색경로 https://www.youtube.com/playlist?list=PLpIPLT0Pf7IqS4as3nefPyGv94r2aY6IT
- [3] 남준우, 「비모수커널추정법에 의한 확률밀도함수의 추정」, 서강대학교, "https://sc.sogang.ac.kr/jnahm/research/density.pdf"
- [4] 데이비드 스피겔할터, 『숫자에 약한 사람들을 위한 통계학 수업』, 권혜승, 김영훈, 웅진지식하우스. 2020.
- [5] 박정식, 윤영선, 박래수, 『현대통계학: 제5판』, 서현정, 다산출판사. 2018.
- [6] 사이온스올, 「도수분포다각형」, 사이언스올, "https://www.scienceall.com/도수분포다각형frequency-distribution-polygon/"
- [7] 사이언스올, 「분포다각형」, 사이언스올, "https://www.scienceall.com/분포다각형distribution-polygon/"
- [8] 장원철, 「데이터로 배우는 통계학」, KMOOC, "http://www.kmooc.kr/courses/course-v1:SNUk+SNU064.020k+2021_T2/course/"
- [9] 존이, 「Truth in Engineering」, 네이버블로그, "https://m.blog.naver.com/PostList.naver?blogId=mykepzzang"
- [10] 차재복, 「정보통신기술용어해설」, 차재복연구실, "http://www.ktword.co.kr/index.php"
- [11] 필로홍, 필로홍의 데이터 노트, "https://drhongdatanote.tistory.com/category/통계%20노트/통계%20개념%20정리"
- [12] 쿠리하라 신이치, 마루야마 아츠치,『통계학도감』, 김선숙, 성안당. 2018.
- [13] 통계청, 「통계용어ㆍ지표의 이해(2015)」, 통계청, "https://www.kostat.go.kr/file_total/2015_korki_tot.pdf"
- [14] 한국정보통신기술협회, 「정보통신용어사전」, TTA, "http://terms.tta.or.kr/main.do"
부분
- [1] 통계의 본질, 「표준오차가 뭔가요? 표준편차랑 다른건가요?」, 통계의 본질, "https://hsm-edu.tistory.com/794"
- [2] KANG, 「표준편차와 표준오차의 차이점」, 통계학 이야기, "https://blog.naver.com/PostView.naver?blogId=vnf3751&logNo=221083269431&redirect=Dlog&widgetTypeCall=true&directAccess=false"